
【题目】(本题满分14分)已知函数![]() .
.
(Ⅰ)若函数![]() 在其定义域上是增函数,求实数
在其定义域上是增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,求出
时,求出![]() 的极值;
的极值;
(Ⅲ)在(Ⅰ)的条件下,若![]() 在
在![]() 内恒成立,试确定
内恒成立,试确定![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)实数![]() 的取值范围是
的取值范围是![]() ;
;
(Ⅱ)极大值![]() ,极小值
,极小值![]() ;(Ⅲ),
;(Ⅲ),![]() 的取值范围是
的取值范围是![]() .
.
【解析】试题分析:(Ⅰ)首先求出函数![]() 的导函数,再由函数
的导函数,再由函数![]() 的单调性得到
的单调性得到![]() 在
在![]() 内恒成立,最后由分离参数法求出实数
内恒成立,最后由分离参数法求出实数![]() 的取值范围;
的取值范围;
(Ⅱ)根据导函数的符号确定函数![]() 的单调区间与极值点,进而求出函数的极大值与极小值.
的单调区间与极值点,进而求出函数的极大值与极小值.
(Ⅲ)设![]() ,则
,则![]() 在
在![]() 内恒成立
内恒成立
等价于![]() 结合(I)的结果,利用导数判断函数
结合(I)的结果,利用导数判断函数![]() 的单调性,并出其最大值,从而求出
的单调性,并出其最大值,从而求出![]() 的取值范围.
的取值范围.
试题解析:
(Ⅰ)解:函数![]() 的定义域为
的定义域为![]() ,
,
则![]() ,
, ![]() 1分
1分
因为函数![]() 在
在![]() 内是增函数,
内是增函数,
所以![]() 在
在![]() 内恒成立 2分
内恒成立 2分
所以, ![]() 在
在![]() 内恒成立 3分
内恒成立 3分
因为当![]() 时,
时, ![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时, 等号成立,
时, 等号成立,
所以实数![]() 的取值范围是
的取值范围是![]() . 5分
. 5分
(Ⅱ)解:当![]() 时,
时, ![]() 7分
7分
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下:
的变化情况如下:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
所以, ![]() 在
在![]() 处取得极大值
处取得极大值![]() ,
,
![]() 在
在![]() 处取得极小值
处取得极小值![]() . 9分
. 9分
(Ⅲ)解:设![]()
![]() 10分
10分
则![]() 11分
11分
由(I)可知![]() ,且
,且![]() ,故
,故![]() ,
,
所以![]() 在
在![]() 内为增函数 12分
内为增函数 12分
因为![]() ,即
,即![]() ,
,
所以,![]() 的取值范围是
的取值范围是![]() 14分
14分


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】 由经验得知,在某商场付款处排队等候付款的人数及概率如下表
排队人数 | 0 | 1 | 2 | 3 | 4 | 5人以上 |
概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(1)至多有2人排队的概率是多少?
(2)至少有2人排队的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,底面ABCD为正方形,平面AED⊥平面ABCD,AB= ![]() EA=
EA= ![]() ED,EF∥BD
ED,EF∥BD 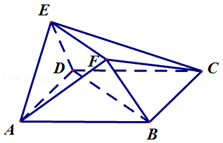
(I)证明:AE⊥CD
(II)在棱ED上是否存在点M,使得直线AM与平面EFBD所成角的正弦值为 ![]() ?若存在,确定点M的位置;若不存在,请说明理由.
?若存在,确定点M的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+![]() ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个偶数组成的数阵排列如下:
2 4 8 14 22 32 …
6 10 16 24 34 … …
12 18 26 36 … … …
20 28 38 … … … …
30 40 … … … … …
42 … … … … … …
… … … … … … …
则第20行第4列的数为( )
A. 546 B. 540 C. 592 D. 598
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣b)lnx+x2在区间[1,e]上单调递增,则实数b的取值范围是( )
A.(﹣∞,﹣3]
B.(﹣∞,2e]
C.(﹣∞,3]
D.(﹣∞,2e2+2e]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com