
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,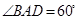 ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.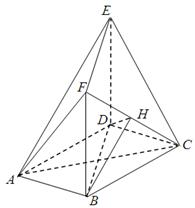
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求直线DH与平面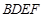 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的大小.
的大小.
(Ⅰ)答案详见解析;(Ⅱ) ;(Ⅲ)
;(Ⅲ) .
.
解析试题分析:(Ⅰ)要证明 平面
平面 ,只需证明
,只需证明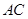 垂直于面
垂直于面 内的两条相交相交直线,由
内的两条相交相交直线,由 是菱形,故
是菱形,故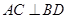 ,再证明
,再证明 ,从而可证明
,从而可证明 平面
平面 ;(Ⅱ)由已知,选三条两两垂直的直线分别为x轴,y轴,z轴,建立空间直角坐标系,表示相关点的坐标,求直线
;(Ⅱ)由已知,选三条两两垂直的直线分别为x轴,y轴,z轴,建立空间直角坐标系,表示相关点的坐标,求直线 的方向向量
的方向向量 坐标,以及面
坐标,以及面 法向量
法向量 的坐标,设直线
的坐标,设直线 与平面
与平面 所成角为
所成角为 ,则
,则 ;(Ⅲ)先求二面角两个半平面的法向量,再求法向量的夹角,通过观察二面角是锐二面角还是钝二面角,决定二面角余弦值的正负,该题中面
;(Ⅲ)先求二面角两个半平面的法向量,再求法向量的夹角,通过观察二面角是锐二面角还是钝二面角,决定二面角余弦值的正负,该题中面 的法向量就是
的法向量就是 ,只需求面
,只需求面
的法向量即可.
试题解析:(Ⅰ)证明:因为四边形 是菱形,所以
是菱形,所以 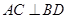 .
.
因为平面 平面
平面 ,且四边形
,且四边形 是矩形,所以
是矩形,所以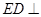 平面
平面 ,
,
又因为 平面
平面 ,所以
,所以  . 因为
. 因为 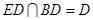 ,所以
,所以  平面
平面 .
.
(Ⅱ)解:设 ,取
,取 的中点
的中点 ,连接
,连接 ,因为四边形
,因为四边形 是矩形,
是矩形,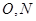 分别为
分别为 的中点,所以
的中点,所以 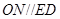 ,又因为
,又因为 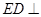 平面
平面 ,所以
,所以  平面
平面 ,由
,由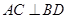 ,得
,得 两两垂直.所以以
两两垂直.所以以 为原点,
为原点, 所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.因为底面
所在直线分别为x轴,y轴,z轴,如图建立空间直角坐标系.因为底面 是边长为2的菱形,
是边长为2的菱形,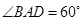 ,
, ,
,
所以  ,
, ,
, ,
, ,
, ,
, ,
, .
.
因为  平面
平面 , 所以平面
, 所以平面 的法向量
的法向量 . 设直线
. 设直线 与平面
与平面 所成角为
所成角为 ,由
,由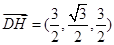 , 得
, 得  ,所以直线
,所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:解答题
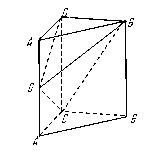
如图,在正三棱柱ABC—A1B1C1中,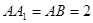 .
.
(1)求直线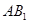 与平面
与平面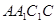 所成角的正弦值;
所成角的正弦值;
(2)在线段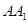 上是否存在点
上是否存在点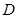 ?使得二面角
?使得二面角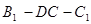 的大小为60°,若存在,求出
的大小为60°,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形, ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com