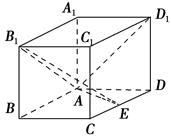
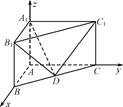
(1)根据题意,在△AOC中,AC=a=2,AO=CO=
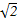
,
所以AC
2=AO
2+CO
2,所以AO⊥CO.
又AO⊥BD,BD∩CO=O,
所以AO⊥平面BCD.
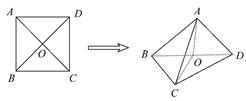
(2)方法一:由(1)知,CO⊥OD,以O为原点,OC,OD所在的直线分别为x轴、y轴建立如图的空间直角坐标系Oxyz,
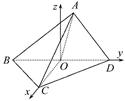
则有O(0,0,0),D(0,
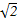
,0),
C(
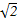
,0,0),B(0,-
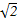
,0).
设A(x
0,0,z
0)(x
0<0),
则

=(x
0,0,z
0),

=(0,
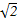
,0).
平面ABD的一个法向量为n=(z
0,0,-x
0).
平面BCD的一个法向量为m=(0,0,1),且二面角A-BD-C的大小为120°,
所以|cos<m,n>|=|cos120°|=

,得
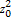
=3
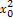
.
因为OA=
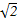
,所以

=
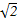
.解得x
0=-

,z
0=
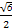
.所以A(-

,0,
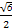
).
平面ABC的一个法向量为l=(1,-1,
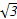
).
设二面角A-BC-D的平面角为θ,
所以cosθ=|cos<l,m>|=|
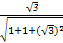
|=

.
所以tanθ=
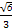
.
所以二面角A-BC-D的正切值为
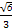
.
方法二:折叠后,BD⊥AO,BD⊥CO.所以∠AOC是二面角A-BD-C的平面角,即∠AOC=120°.在△AOC中,AO=CO=
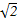
,所以AC=

.
如图,过点A作CO的垂线交CO延长线于点H,
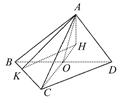
因为BD⊥CO,BD⊥AO,且CO∩AO=O,所以BD⊥平面AOC.因为AH?平面AOC,所以BD⊥AH.
又CO⊥AH,且CO∩BD=O,所以AH⊥平面BCD.所以AH⊥BC.过点A作AK⊥BC,垂足为K,连接HK,因为BC⊥AH,AK∩AH=A,所以BC⊥平面AHK.因为HK?平面AHK,所以BC⊥HK.所以∠AKH为二面角A-BC-D的平面角.
在△AOH中,得AH=
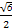
,OH=

,所以CH=CO+OH=
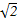
+

=
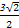
.
在Rt△CHK中,HK=
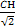
=

,
在Rt△AHK中,tan∠AKH=

=
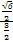
=
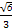
.
所以二面角A-BC-D的正切值为
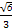
.

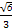
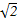 ,
,
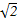 ,0),
,0),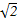 ,0,0),B(0,-
,0,0),B(0,-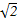 ,0).
,0). =(x0,0,z0),
=(x0,0,z0), =(0,
=(0,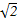 ,0).
,0). ,得
,得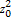 =3
=3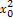 .
.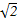 ,所以
,所以 =
=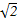 .解得x0=-
.解得x0=- ,z0=
,z0=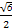 .所以A(-
.所以A(- ,0,
,0,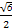 ).
).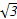 ).
).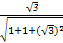 |=
|= .
.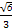 .
.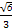 .
.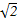 ,所以AC=
,所以AC= .
.
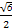 ,OH=
,OH= ,所以CH=CO+OH=
,所以CH=CO+OH=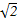 +
+ =
=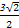 .
.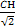 =
= ,
, =
=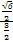 =
=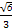 .
.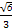 .
.

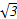 AD,E为CD上一点,且CE=3DE.
AD,E为CD上一点,且CE=3DE.