练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某学生将语文、数学、英语、物理、化学、生物科的作业安排在周六、周日完成，要求每天至少完成两科，且数学、物理作业不在同一天完成，则完成作业的不同顺序种数为______.

    【答案】

    【解析】

    分两类：①一天科，另一天科，第一步，安排数学、物理两科作业，第二步，安排另科一组科，一组科，第三步，完成各科作业.②两天各科，数学、物理两科各一组，另科每组分科，第一步，安排数学、物理两科作业，第二步，安排另科每组科，第三步，完成各科作业.

    分两类：一天科，另一天科或每天各科.

    ①第一步，安排数学、物理两科作业，有种方法；

    第二步，安排另科一组科，一组科，有种方法；

    第三步，完成各科作业，有种方法.

    所以共有种.

    ②两天各科，数学、物理两科各一组，另科每组分科，

    第一步，安排数学、物理两科作业，有种方法；

    第二步，安排另科每组科，有种方法；

    第三步，完成各科作业，有种方法.

    所以共有种.

    综上，共有种.

    故答案为：1200

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校高二年级的数学兴趣小组釆取抽签方式随机分成甲、乙两个小组进行数学解题对抗赛.每组各20人，根据各位学生在第三次数学解题对抗赛中的解题时间（单位：秒）绘制了如下茎叶图：

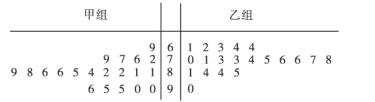
    （1）请评出第三次数学对抗赛的优胜小组，并求出这40位学生完成第三次数学解题对抗赛所需时间的中位数；

    （2）对于（1）中的中位数，根据这40位学生完成第三次数学对抗赛所需时间超过和不超过的人数，完成下面的列联表，并判断能否有的把握认为甲、乙两个小组在此次的数学对抗赛中的成绩有差异？

    超过

    不超过

    总计

    甲组

    乙组

    总计

    附：，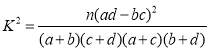

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的焦距为2，且过点．

    （1）求椭圆的方程；

    （2）设为的左焦点，点为直线上任意一点，过点作的垂线交于两点，

    （ⅰ）证明：平分线段（其中为坐标原点）；

    （ⅱ）当取最小值时，求点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB＝4，AD＝2，点E是DC的中点，将△ADE沿AE折起，使平面ADE⊥平面ABCE，连结DB、DC、EB．

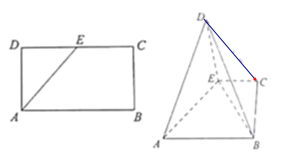
    （1）求证：平面ADE⊥平面BDE；

    （2）求AD与平面BDC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，一个动圆经过点且与直线相切，设该动圆圆心的轨迹为曲线.

    （1）求曲线的方程；

    （2）过点作直线交曲线于，两点，问曲线上是否存在一个定点，使得点在以为直径的圆上？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将四个不同的小球放入三个分别标有1、2、3号的盒子中，不允许有空盒子的放法有多少种？下列结论正确的有（ ）.

    A.B.C.D.18

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线的参数方程为（其中为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）若点在直线上，且，求直线的斜率；

    （2）若，求曲线上的点到直线的距离的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】受传统观念的影响，中国家庭教育过程中对子女教育的投入不遗余力，基础教育消费一直是中国家庭教育的重头戏，升学压力的逐渐增大，特别是对于升入重点学校的重视，导致很多家庭教育支出增长较快，下面是某机构随机抽样调查某二线城市2012-2018年的家庭教育支出的折线图.

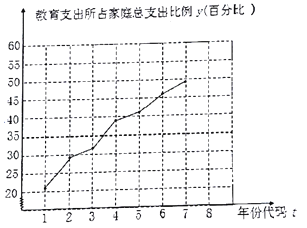
    （附：年份代码1-7分别对应的年份是2012-2018）

    （1）从图中的折线图看出，可用线性回归模型拟合y与t的关系，请求出相关系数r（精确到0.001），并指出是哪一层次的相关性？（相关系数，相关性很强；，相关性一般；，相关性较弱）.

    （2）建立y关于t的回归方程；

    （3）若2019年该地区家庭总支出为10万元，预测家庭教育支出约为多少万元？

    附注：参考数据：，，，，.

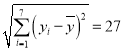    参考公式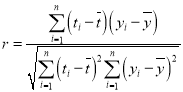：，回归方程，

    其中，.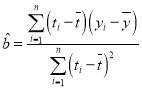

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，不等式的解集是.

    （1）求的解析式；

    （2）不等式组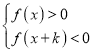的正整数解只有一个，求实数k取值范围；

    （3）若对于任意，不等式恒成立，求t的取值范围.

    查看答案和解析>>

    同步练习册答案