
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() (
(![]() ),过点
),过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() ,
, ![]() ,
, ![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,试求
,试求![]() ,
, ![]() 满足的关系式.
满足的关系式.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)因为离心率![]() ,所以
,所以![]() ,又以
,又以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切,所以
相切,所以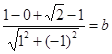 ,再结合
,再结合![]() ,求得
,求得![]() ,
,![]() ,即求得椭圆
,即求得椭圆![]() 标准方程;
标准方程;
(2)①当直线斜率不存在时,直线![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 的交点
的交点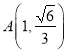 ,
, 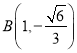 ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() 的关系式为
的关系式为![]() .②当直线的斜率存在时,设点
.②当直线的斜率存在时,设点![]() ,设直线
,设直线![]() ,联立椭圆整理得:
,联立椭圆整理得: ![]() ,根系关系略,所以
,根系关系略,所以![]() 化简得
化简得![]() ,结合韦达定理得
,结合韦达定理得![]() ,所以
,所以![]() ,所以
,所以![]() 的关系式为
的关系式为![]() .
.
试题解析:(1)因为离心率![]() ,所以
,所以![]() ,
,
又因为以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切,
相切,
所以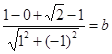 ,即
,即![]()
因为![]() ,
,
所以![]()
所以椭圆![]() 标准方程;
标准方程; ![]()
(2)①当直线斜率不存在时,由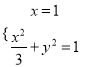 ,解得
,解得![]() ,不妨设
,不妨设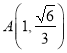 ,
, 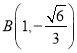 ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 的关系式为
的关系式为![]() .
.
②当直线的斜率存在时,设点![]() ,设直线
,设直线![]() ,联立椭圆整理得:
,联立椭圆整理得: ![]() ,根系关系略,所以
,根系关系略,所以
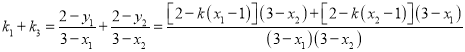
![]()
![]()
![]()
所以![]() ,所以
,所以![]() 的关系式为
的关系式为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与直线
,且与直线![]() 相切,椭圆
相切,椭圆![]() 的对称轴为坐标轴,
的对称轴为坐标轴,![]() 点为坐标原点,
点为坐标原点,![]() 是其一个焦点,又点
是其一个焦点,又点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的标准方程和椭圆
的标准方程和椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 点,交轨迹
点,交轨迹![]() 于
于![]() 两点,设
两点,设![]() 为
为![]() 的面积,
的面积,![]() 为
为![]() 的面积,令
的面积,令![]() 的面积,令
的面积,令![]() ,试求
,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a,b,c,若c=2![]() ,sinB=2sinA.
,sinB=2sinA.
(1)若C=![]() ,求a,b的值;
,求a,b的值;
(2)若cosC=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】pH值是水溶液的重要理化参数。若溶液中氢离子的浓度为[H![]() ](单位:mol/l),则其pH值为-lg[H
](单位:mol/l),则其pH值为-lg[H![]() ]。在标准温度和气压下,若水溶液pH=7,则溶液为中性,pH<7时为酸性,pH>7时为碱性。例如,甲溶液中氢离子浓度为0.0001mol/l,其pH为-1g 0.0001,即pH=4。已知乙溶液的pH=2,则乙溶液中氢离子浓度为______mol/l。若乙溶液中氢离子浓度是丙溶液的两千万倍,则丙溶液的酸碱性为______(填中性、酸性或碱性)。
]。在标准温度和气压下,若水溶液pH=7,则溶液为中性,pH<7时为酸性,pH>7时为碱性。例如,甲溶液中氢离子浓度为0.0001mol/l,其pH为-1g 0.0001,即pH=4。已知乙溶液的pH=2,则乙溶液中氢离子浓度为______mol/l。若乙溶液中氢离子浓度是丙溶液的两千万倍,则丙溶液的酸碱性为______(填中性、酸性或碱性)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某校学生的视力情况,现采用随机抽样的方式从该校的![]() 两班中各抽5名学生进行视力检测,检测的数据如下:
两班中各抽5名学生进行视力检测,检测的数据如下:
![]() 班5名学生的视力检测结果是:
班5名学生的视力检测结果是: ![]() .
.
![]() 班5名学生的视力检测结果是:
班5名学生的视力检测结果是: ![]() .
.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?并计算![]() 班的5名学生视力的方差;
班的5名学生视力的方差;
(2)现从![]() 班上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于
班上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6名奥运会志愿者,其中志愿者![]() 通晓日语,
通晓日语, ![]() 通晓俄语,
通晓俄语, ![]() 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求![]() 被选中的概率;
被选中的概率;
(2)求![]() 和
和![]() 不全被选中的概率;
不全被选中的概率;
(3)若6名奥运会志愿者每小时派两人值班,现有两名只会日语的运动员到来,求恰好遇到![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 外的有一点
外的有一点![]() ,过点
,过点![]() 作直线
作直线![]() .
.
(1)当直线![]() 过圆心
过圆心![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,求直线
相切时,求直线![]() 的方程;
的方程;
(3)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求直线
时,求直线![]() 被圆
被圆![]() 所截得的弦长.
所截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
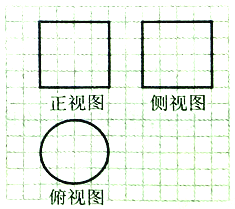
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三视图,第一次切削,将该毛坯得到一个表面积最大的长方体;第二次切削沿长方体的对角面刨开,得到两个三棱柱;第三次切削将两个三棱柱分别沿棱和表面的对角线刨开得到两个鳖臑和两个阳马,则阳马与鳖臑的体积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com