Question

【题目】已知四棱锥P－ABCD的底面为等腰梯形, AB∥CD,AC⊥BD,垂足为H, PH是四棱锥的高,E为AD中点,设

1)证明：PE⊥BC；

2)若∠APB＝∠ADB＝60°，求直线PA与平面PEH所成角的正弦值．

Answer 1

【答案】(1)见解析;(2).

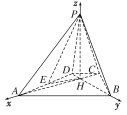
【解析】分析：（1）以H为原点，HA，HB，HP所在直线分别为x，y，z轴，建立空间直角

坐标系，利用向量法能证明PE⊥BC；

（2）求出平面PEH的法向量和＝(1,0，－1)，利用向量法能求出直线PA与平面PEH所成角的正弦值．

详解：以H为原点，HA，HB，HP所在直线分别为x，y，z轴，建立空间直角坐标系如图，则A(1,0,0)，B(0,1,0)，

(1)证明：设C(m,0,0)，P(0,0，n)(m<0，n>0)，则D(0，m,0)，E(，，0)．

可得＝(，，－n)，＝(m，－1,0)． 因为·＝－＋0＝0，

所以PE⊥BC.

(2)由已知条件可得m＝－，n＝1，

故C(－，0,0)，D(0，－，0)，E(，－，0)，

P(0，0,1)．设n＝(x，y，z)为平面PEH的法向量，

则即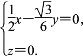

因此可以取n＝(1，，0)．

由＝(1,0，－1)，可得|cos〈，n〉|＝，

所以直线PA与平面PEH所成角的正弦值为.