
【题目】每年春晚都是万众瞩目的时刻,这些节目体现的文化内涵、历史背景等反映了社会的进步.国家的富强,人民生活水平的提高等.某学校高三年级主任开学初为了解学生在看春晚后对节目体现的文化内涵、历史背景等是否会在今年的高考题中体现进行过思考,特地随机抽取100名高三学生(其中文科学生50,理科学生50名),进行了调查.统计数据如表所示(不完整):
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | |
理科学生 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有![]() 的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
(2)①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人,记这4人中“文科学生”的人数为![]() ,试求
,试求![]() 的分布列与数学期望;
的分布列与数学期望;
②现设计一份试卷(题目知识点来自春晚相关知识整合与变化),假设“思考过”的学生及格率为![]() ,“没有思考过”的学生的及格率为
,“没有思考过”的学生的及格率为![]() .现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
附参考公式: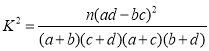 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)列联表见解析,有;(2)①见解析;②![]() .
.
【解析】
(1)根据题意,得出![]() 的列联表,利用公式求的
的列联表,利用公式求的![]() 的值,即可得出结论;
的值,即可得出结论;
(2)①由题意,得出所以![]() 的所有可能取值为
的所有可能取值为![]() ,取得随机变量取每个值对应的概率,得出分布列,利用期望的公式,即可求解.
,取得随机变量取每个值对应的概率,得出分布列,利用期望的公式,即可求解.
②设“思考过”的学生的及格率![]() ;“没有思考过”的学生的及格率
;“没有思考过”的学生的及格率![]() ,根据独立事件的概率计算公式,即可求解.
,根据独立事件的概率计算公式,即可求解.
(1)填表如下:
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | 50 |
理科学生 | 30 | 20 | 50 |
总计 | 70 | 30 | 100 |
由上表得,![]() 的观测值
的观测值![]() ,
,
故有![]() 的把握认为看春晚节目后是否会思考与文理科学生有关.
的把握认为看春晚节目后是否会思考与文理科学生有关.
(2)①由题意,得抽取的100名学生中“思考过”的有文科学生40人,理科学生30人,所以抽取7人中文科学生有4人,理科学生有3人,所以![]() 的所有可能取值为1,2,3,4.
的所有可能取值为1,2,3,4.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
所以![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
P |
|
|
|
|
故数学期望为![]() .
.
②设“思考过”的学生的及格率为![]() ,则
,则![]() ;“没有思考过”的学生的及格率为
;“没有思考过”的学生的及格率为![]() ,则
,则![]() ,所以两人至少有一个及格的概率为
,所以两人至少有一个及格的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,天花板上挂着3串玻璃球,射击玻璃球规则:每次击中1球,每串中下面球没击中,上面球不能击中,则把这6个球全部击中射击方法数是( )
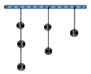
A.78B.60C.48D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物小组为了研究温度对某种酶的活性的影响进行了一组实验,得到的实验数据经整理得到如下的折线图:
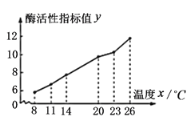
(1)由图可以看出,这种酶的活性![]() 与温度
与温度![]() 具有较强的线性相关性,请用相关系数加以说明;
具有较强的线性相关性,请用相关系数加以说明;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测当温度为
的线性回归方程,并预测当温度为![]() 时,这种酶的活性指标值.(计算结果精确到0.01)
时,这种酶的活性指标值.(计算结果精确到0.01)
参考数据:![]() ,
,![]() ,
,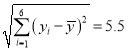 ,
,![]() .
.
参考公式:相关系数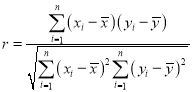 .
.
回归直线方程![]() ,
,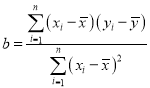 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的四个命题:
①线性回归直线必过样本数据的中心点(![]() );
);
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于
就越接近于![]() .
.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知球![]() 是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)
是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)![]() 的外接球,
的外接球,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,过点
,过点![]() 作球
作球![]() 的截面,则所得截面圆面积的取值范围是( )
的截面,则所得截面圆面积的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF![]() a,以下结论正确的有( )
a,以下结论正确的有( )

A.AC⊥BE
B.点A到△BEF的距离为定值
C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的![]()
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB![]() 平面BEC,BE
平面BEC,BE![]() EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
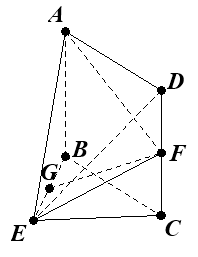
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调查.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
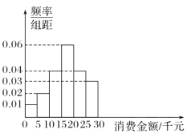
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”
列联表,并判断有多大把握认为“网购迷与性别有关系”
男 | 女 | 总计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
总计 | 100 |
附:![]() .
.
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com