
ЎҫМвДҝЎҝСфВнәНұоДһЈЁbienaoЈ©КЗЎ¶ҫЕХВЛгКхЎӨЙМ№ҰЎ·Ап¶ФБҪЦЦЧ¶МеөДіЖОҪ.ИзНјЛщКҫЈ¬ИЎТ»ёціӨ·ҪМеЈ¬°ҙПВНјРұёоТ»·ЦОӘ¶юЈ¬өГБҪёцДЈТ»СщөДИэАвЦщЈ¬іЖОӘЗө¶ВЈЁИзНјЈ©.ФЩСШЖдЦРТ»ёцЗө¶ВөДТ»ёц¶ҘөгУлПа¶ФөДАвЖКҝӘЈ¬өГЛДАвЧ¶әНИэАвЧ¶ёчТ»ёцЈ¬УРТ»АвУлөЧГжҙ№ЦұөДЛДАвЧ¶іЖОӘСфВнЈЁЛДАвЧ¶![]() Ј©УаПВИэАвЧ¶іЖОӘұоДһЈЁИэАвЧ¶
Ј©УаПВИэАвЧ¶іЖОӘұоДһЈЁИэАвЧ¶![]() Ј©ИфҪ«ДііӨ·ҪМеСШЙПКцЗРёо·Ҫ·ЁөГөҪТ»ёцСфВнТ»ёцұоДһЈ¬ЗТёГСфВнөДХэКУНјәНұоДһөДІаКУНјИзНјЛщКҫЈ¬ФтҝЙЗуіцёГСфВнәНұоДһөДұнГж»эЦ®әНОӘЈЁ Ј©
Ј©ИфҪ«ДііӨ·ҪМеСШЙПКцЗРёо·Ҫ·ЁөГөҪТ»ёцСфВнТ»ёцұоДһЈ¬ЗТёГСфВнөДХэКУНјәНұоДһөДІаКУНјИзНјЛщКҫЈ¬ФтҝЙЗуіцёГСфВнәНұоДһөДұнГж»эЦ®әНОӘЈЁ Ј©

A.![]() B.
B.![]()
C.![]() D.
D.![]()
 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘНЦФІ![]() УлЕЧОпПЯ
УлЕЧОпПЯ![]() УР№ІН¬өДҪ№өг
УР№ІН¬өДҪ№өг![]() Ј¬ЗТБҪЗъПЯөД№«№ІөгөҪ
Ј¬ЗТБҪЗъПЯөД№«№ІөгөҪ![]() өДҫаАлКЗЛьөҪЦұПЯ
өДҫаАлКЗЛьөҪЦұПЯ![]() ЈЁөг
ЈЁөг![]() ФЪҙЛЦұПЯУТІаЈ©өДҫаАлөДТ»°л.
ФЪҙЛЦұПЯУТІаЈ©өДҫаАлөДТ»°л.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©Йи![]() ОӘЧшұкФӯөгЈ¬ЦұПЯ
ОӘЧшұкФӯөгЈ¬ЦұПЯ![]() №эөг
№эөг![]() ЗТУлНЦФІҪ»УЪ
ЗТУлНЦФІҪ»УЪ![]() БҪөгЈ¬ТФ
БҪөгЈ¬ТФ![]() ОӘБЪұЯЧчЖҪРРЛДұЯРО
ОӘБЪұЯЧчЖҪРРЛДұЯРО![]() .КЗ·сҙжФЪЦұПЯ
.КЗ·сҙжФЪЦұПЯ![]() Ј¬К№өг
Ј¬К№өг![]() ВдФЪНЦФІ
ВдФЪНЦФІ![]() »тЕЧОпПЯ
»тЕЧОпПЯ![]() ЙПЈҝИфҙжФЪЈ¬Зуіцөг
ЙПЈҝИфҙжФЪЈ¬Зуіцөг![]() ЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
ЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЕЧОпПЯCЈә![]() өДҪ№өгОӘFЈ¬QКЗЕЧОпПЯЙПөДТ»өгЈ¬
өДҪ№өгОӘFЈ¬QКЗЕЧОпПЯЙПөДТ»өгЈ¬![]() Ј®
Ј®
ЈЁўсЈ©ЗуЕЧОпПЯCөД·ҪіМЈ»
ЈЁўтЈ©№эөг![]() ЧчЦұПЯlУлЕЧОпПЯCҪ»УЪMЈ¬NБҪөгЈ¬ФЪxЦбЙПКЗ·сҙжФЪТ»өгAЈ¬К№өГxЦбЖҪ·Ц
ЧчЦұПЯlУлЕЧОпПЯCҪ»УЪMЈ¬NБҪөгЈ¬ФЪxЦбЙПКЗ·сҙжФЪТ»өгAЈ¬К№өГxЦбЖҪ·Ц![]() ЈҝИфҙжФЪЈ¬ЗуіцөгAөДЧшұкЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
ЈҝИфҙжФЪЈ¬ЗуіцөгAөДЧшұкЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЦұПЯ
ЦРЈ¬ЦұПЯ![]() өДІОКэ·ҪіМОӘ
өДІОКэ·ҪіМОӘ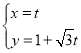 ЈЁ
ЈЁ![]() ОӘІОКэЈ©Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬ТФ
ОӘІОКэЈ©Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬ТФ![]() ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ
ЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() ПаҪ»УЪ
ПаҪ»УЪ![]() БҪөгЈ¬Ул
БҪөгЈ¬Ул![]() ЦбПаҪ»УЪөг
ЦбПаҪ»УЪөг![]() .
.
ЈЁ1Ј©ЗуЦұПЯ![]() өДЖХНЁ·ҪіМәНЗъПЯ
өДЖХНЁ·ҪіМәНЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©Зу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЛДАвЧ¶P©ҒABCDЦРЈ¬ТСЦӘPAЎНЖҪГжABCDЈ¬ЎчABCОӘөИұЯИэҪЗРОЈ¬PA=2AB=2Ј¬ACЎНCDЈ¬PDУлЖҪГжPACЛщіЙҪЗөДУаПТЦөОӘ![]() .
.
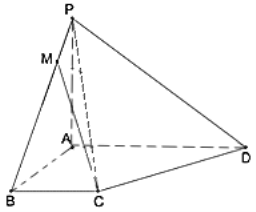
ЈЁ1Ј©ЦӨГчЈә![]() ЖҪГжPADЈ»
ЖҪГжPADЈ»
ЈЁ2Ј©өгMОӘPBЙПТ»өгЈ¬ЗТ![]() Ј¬КФЕР¶ПөгMөДО»ЦГ.
Ј¬КФЕР¶ПөгMөДО»ЦГ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСфВнәНұоДһЈЁbienaoЈ©КЗЎ¶ҫЕХВЛгКхЎӨЙМ№ҰЎ·Ап¶ФБҪЦЦЧ¶МеөДіЖОҪ.ИзНјЛщКҫЈ¬ИЎТ»ёціӨ·ҪМеЈ¬°ҙПВНјРұёоТ»·ЦОӘ¶юЈ¬өГБҪёцДЈТ»СщөДИэАвЦщЈ¬іЖОӘЗө¶ВЈЁИзНјЈ©.ФЩСШЖдЦРТ»ёцЗө¶ВөДТ»ёц¶ҘөгУлПа¶ФөДАвЖКҝӘЈ¬өГЛДАвЧ¶әНИэАвЧ¶ёчТ»ёцЈ¬УРТ»АвУлөЧГжҙ№ЦұөДЛДАвЧ¶іЖОӘСфВнЈЁЛДАвЧ¶![]() Ј©УаПВИэАвЧ¶іЖОӘұоДһЈЁИэАвЧ¶
Ј©УаПВИэАвЧ¶іЖОӘұоДһЈЁИэАвЧ¶![]() Ј©ИфҪ«ДііӨ·ҪМеСШЙПКцЗРёо·Ҫ·ЁөГөҪТ»ёцСфВнТ»ёцұоДһЈ¬ЗТёГСфВнөДХэКУНјәНұоДһөДІаКУНјИзНјЛщКҫЈ¬ФтҝЙЗуіцёГСфВнәНұоДһөДұнГж»эЦ®әНОӘЈЁ Ј©
Ј©ИфҪ«ДііӨ·ҪМеСШЙПКцЗРёо·Ҫ·ЁөГөҪТ»ёцСфВнТ»ёцұоДһЈ¬ЗТёГСфВнөДХэКУНјәНұоДһөДІаКУНјИзНјЛщКҫЈ¬ФтҝЙЗуіцёГСфВнәНұоДһөДұнГж»эЦ®әНОӘЈЁ Ј©

A.![]() B.
B.![]()
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіБ¬ЛшІНМьРВөкҝӘТөЈ¬ҙтЛгҫЩ°мТ»ҙОКіЖ·Ҫ»ТЧ»бЈ¬ХРҙэРВАП№ЛҝНКФіФ.ПоДҝҫӯАнНЁ№эІйФДЧоҪь![]() ҙОКіЖ·Ҫ»ТЧ»бІО»бИЛКэ
ҙОКіЖ·Ҫ»ТЧ»бІО»бИЛКэ![]() ЈЁНтИЛЈ©УлІНМьЛщУГФӯІДБПКэБҝ
ЈЁНтИЛЈ©УлІНМьЛщУГФӯІДБПКэБҝ![]() ЈЁҙьЈ©Ј¬өГөҪИзПВНіјЖұнЈә
ЈЁҙьЈ©Ј¬өГөҪИзПВНіјЖұнЈә
өЪТ»ҙО | өЪ¶юҙО | өЪИэҙО | өЪЛДҙО | өЪОеҙО | |
ІО»бИЛКэЈЁНтИЛЈ© |
|
|
|
|
|
ФӯІДБПЈЁҙьЈ© |
|
|
|
|
|
ЈЁ1Ј©ёщҫЭЛщёш![]() ЧйКэҫЭЈ¬Зуіц
ЧйКэҫЭЈ¬Зуіц![]() №ШУЪ
№ШУЪ![]() өДПЯРФ»Ш№й·ҪіМ
өДПЯРФ»Ш№й·ҪіМ![]() Ј»
Ј»
ЈЁ2Ј©ТСЦӘ№әВтФӯІДБПөД·СУГ![]() ЈЁФӘЈ©УлКэБҝ
ЈЁФӘЈ©УлКэБҝ![]() ЈЁҙьЈ©өД№ШПөОӘ
ЈЁҙьЈ©өД№ШПөОӘ![]() Ј¬Н¶ИлК№УГөДГҝҙьФӯІДБППаУҰөДПъКЫКХИлОӘ
Ј¬Н¶ИлК№УГөДГҝҙьФӯІДБППаУҰөДПъКЫКХИлОӘ![]() ФӘЈ¬¶аУаөДФӯІДБПЦ»ДЬОЮіҘ·ө»№Ј¬ҫЭПӨұҫҙОҪ»ТЧҙу»бҙуФјУР
ФӘЈ¬¶аУаөДФӯІДБПЦ»ДЬОЮіҘ·ө»№Ј¬ҫЭПӨұҫҙОҪ»ТЧҙу»бҙуФјУР![]() НтИЛІОјУЈ¬ёщҫЭЈЁ1Ј©ЦРЗуіцөДПЯРФ»Ш№й·ҪіМЈ¬ФӨІвІНМьУҰ№әВт¶аЙЩҙьФӯІДБПЈ¬ІЕДЬ»сөГЧоҙуАыИуЈ¬ЧоҙуАыИуКЗ¶аЙЩЈҝЈЁЧўЈәАыИу
НтИЛІОјУЈ¬ёщҫЭЈЁ1Ј©ЦРЗуіцөДПЯРФ»Ш№й·ҪіМЈ¬ФӨІвІНМьУҰ№әВт¶аЙЩҙьФӯІДБПЈ¬ІЕДЬ»сөГЧоҙуАыИуЈ¬ЧоҙуАыИуКЗ¶аЙЩЈҝЈЁЧўЈәАыИу![]() ПъКЫКХИл
ПъКЫКХИл![]() ФӯІДБП·СУГЈ©.
ФӯІДБП·СУГЈ©.
ІОҝј№«КҪЈә Ј¬
Ј¬![]() .
.
ІОҝјКэҫЭЈә![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝУРПЮёцФӘЛШЧйіЙөДјҜәП![]() Ј¬
Ј¬![]() Ј¬јЗјҜәП
Ј¬јЗјҜәП![]() ЦРөДФӘЛШёцКэОӘ
ЦРөДФӘЛШёцКэОӘ![]() Ј¬јҙ
Ј¬јҙ![]() .¶ЁТе
.¶ЁТе![]() Ј¬јҜәП
Ј¬јҜәП![]() ЦРөДФӘЛШёцКэјЗОӘ
ЦРөДФӘЛШёцКэјЗОӘ![]() Ј¬өұ
Ј¬өұ![]() КұЈ¬іЖјҜәП
КұЈ¬іЖјҜәП![]() ҫЯУРРФЦК
ҫЯУРРФЦК![]() .
.
ЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј¬ЕР¶ПјҜәП
Ј¬ЕР¶ПјҜәП![]() Ј¬
Ј¬![]() КЗ·сҫЯУРРФЦК
КЗ·сҫЯУРРФЦК![]() Ј¬ІўЛөГчАнУЙЈ»
Ј¬ІўЛөГчАнУЙЈ»
ЈЁ2Ј©ЙијҜәП![]() Ј¬
Ј¬![]() ЗТ
ЗТ![]() (
(![]() )Ј¬ИфјҜәП
)Ј¬ИфјҜәП![]() ҫЯУРРФЦК
ҫЯУРРФЦК![]() Ј¬Зу
Ј¬Зу![]() өДЧоҙуЦөЈ»
өДЧоҙуЦөЈ»
ЈЁ3Ј©ЙијҜәП![]() Ј¬ЖдЦРКэБР
Ј¬ЖдЦРКэБР![]() ОӘөИұИКэБРЈ¬
ОӘөИұИКэБРЈ¬![]() (
(![]() )ЗТ№«ұИОӘУРАнКэЈ¬ЕР¶ПјҜәП
)ЗТ№«ұИОӘУРАнКэЈ¬ЕР¶ПјҜәП![]() КЗ·сҫЯУРРФЦК
КЗ·сҫЯУРРФЦК![]() ІўЛөГчАнУЙ.
ІўЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТӘАыУГТ»°лҫ¶ОӘ![]() өДФІРОЦҪЖ¬ЦЖЧчИэАвЧ¶РО°ьЧ°әР.ТСЦӘёГЦҪЖ¬өДФІРДОӘ
өДФІРОЦҪЖ¬ЦЖЧчИэАвЧ¶РО°ьЧ°әР.ТСЦӘёГЦҪЖ¬өДФІРДОӘ![]() Ј¬ПИТФ
Ј¬ПИТФ![]() ОӘЦРРДЧчұЯіӨОӘ
ОӘЦРРДЧчұЯіӨОӘ![]() ЈЁөҘО»Јә
ЈЁөҘО»Јә![]() Ј©өДөИұЯИэҪЗРО
Ј©өДөИұЯИэҪЗРО![]() Ј¬ФЩ·ЦұрФЪФІ
Ј¬ФЩ·ЦұрФЪФІ![]() ЙПИЎИэёцөг
ЙПИЎИэёцөг![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬К№
Ј¬К№![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ·ЦұрКЗТФ
·ЦұрКЗТФ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘөЧұЯөДөИСьИэҪЗРО.СШРйПЯјфҝӘәуЈ¬·ЦұрТФ
ОӘөЧұЯөДөИСьИэҪЗРО.СШРйПЯјфҝӘәуЈ¬·ЦұрТФ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ОӘХЫәЫХЫЖр
ОӘХЫәЫХЫЖр![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬К№өГ
Ј¬К№өГ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ЦШәПУЪөг
ЦШәПУЪөг![]() Ј¬јҙҝЙөГөҪХэИэАвЧ¶
Ј¬јҙҝЙөГөҪХэИэАвЧ¶![]() .
.
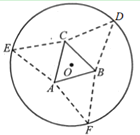

ЈЁ1Ј©ИфИэАвЧ¶![]() КЗХэЛДГжМеЈ¬Зу
КЗХэЛДГжМеЈ¬Зу![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ЗуИэАвЧ¶![]() өДМе»э
өДМе»э![]() өДЧоҙуЦөЈ¬ІўЦёіцПаУҰ
өДЧоҙуЦөЈ¬ІўЦёіцПаУҰ![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com