
【题目】定义在(0,+∞)的函数f(x)满足如下三个条件:
①对于任意正实数a、b,都有f(ab)=f(a)+f(b)-1;
②f(2)=0;
③x>1时,总有f(x)<1.
(1)求f(1)及![]() 的值;
的值;
(2)求证:函数f(x)在(0,+∞)上是减函数;
(3)如果存在正数k,使关于x的方程f(kx)+f(2-x)=-1有解,求正实数k的取值范围.
【答案】(1)f(1)=1;f(![]() )=2;(2)详见解析;(3)[8,+∞).
)=2;(2)详见解析;(3)[8,+∞).
【解析】
(1)令a=b=1,a=2,b![]() ,即可求得f(1)及
,即可求得f(1)及![]() 的值;
的值;
(2)当x>1时,f(x)<1,根据函数单调性的定义讨论函数的单调性;
(3)把f(kx)+f(2﹣x)根据条件转化为f[kx(2﹣x)]﹣1,根据函数的单调性把函数值转化为自变量x的方程,分离参数转化我求函数的值域即可得到所求范围.
解:(1)令a=b=1得f(1)=2f(1)-1,
即有f(1)=1;
令a=2,b=![]() ,可得f(1)=f(2)+f(
,可得f(1)=f(2)+f(![]() )-1=f(
)-1=f(![]() )-1=1,
)-1=1,
即有f(![]() )=2;
)=2;
(2)证明:设0<x1<x2,可得![]() >1,
>1,
可得f(![]() )<1,
)<1,
由f(x2)=f(x1![]() )=f(x1)+f(
)=f(x1)+f(![]() )-1<f(x1),
)-1<f(x1),
可得函数f(x)在(0,+∞)上是减函数;
(3)由f(4)=2f(2)-1=-1,
f(8)=f(2)+f(4)-1=-2,
可得关于x的方程f(kx)+f(2-x)=-1即为f(kx(2-x))=-2=f(8),
函数f(x)在(0,+∞)上是减函数,
可得kx(2-x)=8在0<x<2有解,
即有k=![]() ,
,
由0<x<2可得x(2-x)∈(0,1],
则k的范围是[8,+∞).


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,设倾斜角为α的直线L: ![]() (T为参数)与曲线C:
(T为参数)与曲线C: ![]() (φ为参数)相交于不同的两点A,B.
(φ为参数)相交于不同的两点A,B.
(1)若α= ![]() ,若以坐标原点为极点,x轴的正半轴为极轴,求直线AB的极坐标方程;
,若以坐标原点为极点,x轴的正半轴为极轴,求直线AB的极坐标方程;
(2)若直线的斜率为 ![]() ,点P(2,
,点P(2, ![]() ),求|PA||PB|的值.
),求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
人员编号 | 1 | 2 | 3 | 4 | 5 |
(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
人员编号 | 6 | 7 | 8 | 9 | 10 |
(x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(1)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(2)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m﹣n,求随机变量ξ的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,梯形ABCD中,AD∥BC,∠C= ![]() ,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF.
,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF. 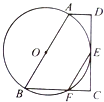
(1)求证:AD+BC=AB;
(2)求证:EF是AD与AB的等比中项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,已知某曲线C的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求该曲线C的直角坐标系方程及离心率![]()
(2)已知点![]() 为曲线C上的动点,求点
为曲线C上的动点,求点![]() 到直线
到直线![]() 的距离的最大值。
的距离的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com