
如图已知抛物线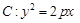 的焦点坐标为
的焦点坐标为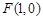 ,过
,过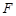 的直线交抛物线
的直线交抛物线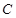 于
于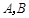 两点,直线
两点,直线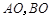 分别与直线
分别与直线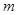 :
: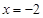 相交于
相交于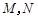 两点.
两点.
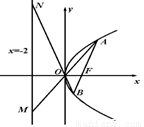
(1)求抛物线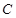 的方程;
的方程;
(2)证明△ABO与△MNO的面积之比为定值.
(1)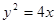 ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】
试题分析:本题主要考查抛物线、直线的方程,以及直线与抛物线的位置关系,突出解析几何的基本思想和方法的考查:如数形结合思想、坐标化方法等.第一问,利用抛物线的标准方程,利用焦点坐标求出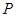 ,代入即可;第二问,讨论直线
,代入即可;第二问,讨论直线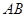 垂直和不垂直
垂直和不垂直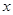 轴2种情况,当直线
轴2种情况,当直线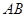 垂直于
垂直于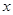 轴时,2个三角形相似,面积比为定值,当直线
轴时,2个三角形相似,面积比为定值,当直线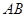 不垂直于
不垂直于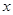 轴时,设出直线
轴时,设出直线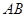 的方程,设出
的方程,设出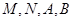 四个点坐标,利用直线
四个点坐标,利用直线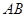 与抛物线相交列出方程组,消参得到方程,利用两根之积得
与抛物线相交列出方程组,消参得到方程,利用两根之积得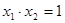 为定值,而面积比值与
为定值,而面积比值与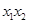 有关,所以也为定值.
有关,所以也为定值.
试题解析:(1)由焦点坐标为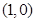 可知
可知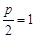
所以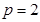 ,所以抛物线
,所以抛物线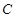 的方程为
的方程为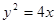 5分
5分
(2)当直线垂直于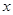 轴时,
轴时,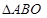 与
与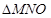 相似,
相似,
所以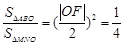 , 7分
, 7分
当直线与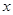 轴不垂直时,设直线AB方程为
轴不垂直时,设直线AB方程为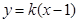 ,
,
设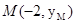 ,
,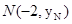 ,
,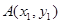 ,
,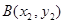 ,
,
解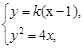 整理得
整理得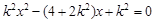 ,
9分
,
9分
所以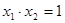 ,
10分
,
10分
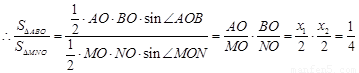 ,
,
综上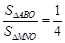 12分
12分
考点:1.抛物线的标准方程;2.直线方程;3.根与系数关系;4.三角形面积公式.


科目:高中数学 来源: 题型:
 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为| π |
| 3 |
| OG |
| OH |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省高三上学期第三次统练文科数学试卷(解析版) 题型:解答题
如图,已知抛物线 的焦点为F,过F的直线交抛物线于M、N两点,其准线
的焦点为F,过F的直线交抛物线于M、N两点,其准线 与x轴交于K点.
与x轴交于K点.

(1)求证:KF平分∠MKN;
(2)O为坐标原点,直线MO、NO分别交准线于点P、Q,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三5月高考三轮模拟文科数学试卷(解析版) 题型:解答题
如图,已知抛物线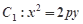 的焦点在抛物线
的焦点在抛物线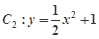 上.
上.
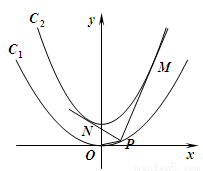
(1)求抛物线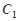 的方程及其准线方程;
的方程及其准线方程;
(2)过抛物线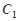 上的动点
上的动点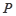 作抛物线
作抛物线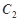 的两条切线
的两条切线 、
、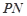 , 切点为
, 切点为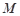 、
、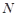 .若
.若 、
、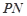 的斜率乘积为
的斜率乘积为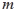 ,且
,且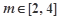 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com