
(本小题满分13分)
已知数列{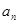 }满足
}满足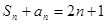 ,
,
(I)写出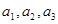 ,并推测
,并推测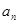 的表达式;
的表达式;
(II)用数学归纳法证明所得的结论。
(Ⅰ) 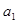 =
= ,
, 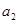 =
=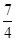 ,
, 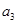 =
=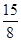 , 猜测
, 猜测 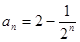 。(Ⅱ)见解析。
。(Ⅱ)见解析。
解析试题分析: (1)根据数列的前几项来归纳猜想得到结论。
(2)在第一问的基础上,进一步运用数学归纳法来加以证明即可。
解: (Ⅰ) 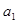 =
= ,
, 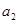 =
=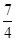 ,
, 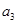 =
=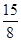 , 猜测
, 猜测 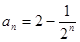 (4分)
(4分)
(Ⅱ) ①由(Ⅰ)已得当n=1时,命题成立;
②假设 时,命题成立,即
时,命题成立,即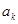 =2-
=2-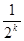 , (6分)
, (6分)
那么当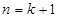 时,
时, 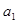 +
+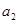 +……+
+……+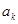 +2
+2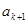 =2(k+1)+1,
=2(k+1)+1,
且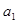 +
+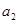 +……+
+……+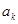 =2k+1-
=2k+1-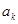 (8分)
(8分)
∴2k+1-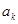 +2ak+1=2(k+1)+1=2k+3,
+2ak+1=2(k+1)+1=2k+3,
∴2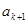 =2+2-
=2+2-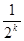 ,
, 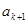 =2-
=2-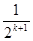 ,
,
即当n=k+1时,命题成立.
根据①②得n∈N+ , 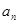 =2-
=2-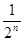 都成立 (13分)
都成立 (13分)
考点:本题主要考查了数列的归纳猜想思想的运用。以及运用数学归纳法求证结论的成立与否。
点评:解决该试题的关键是猜想的正确性,以及和运用数学归纳法证明命题时,要注意假设的运用,推理论证得到证明。


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:解答题
(本小题12分) 正项数列{an}满足a1=2,点An(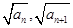 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(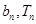 )在直线y=-
)在直线y=-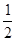 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。
①求数列{an}、{bn}的通项公式;
②设Cn=anbn,证明 Cn+1<Cn
③若m-7anbn>0恒成立,求正整数m的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)数列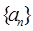 中,
中,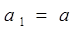 ,
, 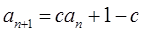
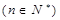
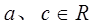
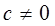
(1)求证: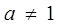 时,
时, 是等比数列,并求
是等比数列,并求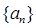 通项公式。
通项公式。
(2)设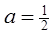 ,
,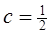 ,
,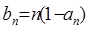
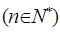 求:数列
求:数列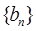 的前n项的和
的前n项的和 。
。
(3)设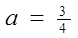 、
、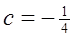 、
、 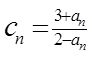 。记
。记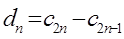 ,数列
,数列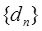 的前n项和
的前n项和 。证明:
。证明: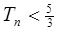
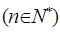 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
投掷一枚均匀硬币2次,记2次都是正面向上的概率为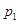 ,恰好
,恰好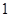 次正面向上的概率为
次正面向上的概率为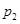 ;等比数列
;等比数列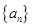 满足:
满足: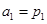 ,
,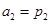
(I)求等比数列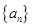 的通项公式;
的通项公式;
(II)设等差数列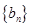 满足:
满足: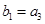 ,
,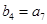 ,求等差数列
,求等差数列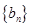 的前
的前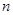 项和
项和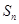 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)已知数列 中,
中, ,
,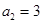 ,其前
,其前 项和
项和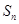 满足
满足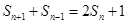 (
(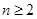 ,
,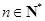 ).
).
(Ⅰ)求证:数列 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)设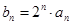 , 求数列
, 求数列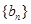 的前
的前 项和
项和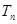 ;
;
(Ⅲ)设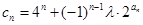 (
(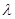 为非零整数,
为非零整数,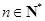 ),试确定
),试确定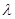 的值,使得对任意
的值,使得对任意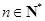 ,有
,有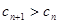 恒成立.
恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com