
ЁОЬтФПЁПББОЉЪаФГФъ11дТ1ШеЁЊ20ШеМрВтзюИпзюЕЭЮТЖШМАВюжЕЪ§ОнШчЯТ:
ШеЦк | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
зюИпЮТЖШ(Ёц) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
зюЕЭЮТЖШ(Ёц) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
ВюжЕ(Ёц) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
ЃЈЂёЃЉЭъГЩЯТУцЕФЦЕТЪЗжВМБэМАЦЕТЪЗжВМжБЗНЭМЃЌВЂаДГіЦЕТЪЗжВМжБЗНЭМжа![]() ЕФжЕЃЛ
ЕФжЕЃЛ

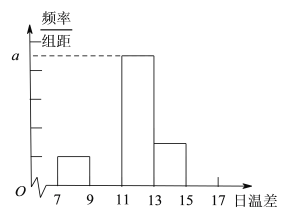
ЃЈЂђЃЉДгШеЮТВюДѓгкЕШгк![]() ЕФетаЉЬьжаЃЌЫцЛњбЁШЁ2Ьь.ЧѓетСНЬьжажСЩйгавЛЬьЕФЮТВюдкЧјМф
ЕФетаЉЬьжаЃЌЫцЛњбЁШЁ2Ьь.ЧѓетСНЬьжажСЩйгавЛЬьЕФЮТВюдкЧјМф![]() ФкЕФИХТЪ.
ФкЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛ![]() .
.
ЃЈ2ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЬтжаЫљИјЕФБэИёЃЌЧѓГіУПЬьЕФЮТВюЃЌЪ§ГіТфдк![]() ФкЕФЦЕЪ§ЃЌРћгУЙЋЪНЧѓЕУЦЕТЪЃЌЭъГЩЦЕТЪЗжВМБэЃЌЭъЩЦжБЗНЭМЃЌРћгУжБЗНЭМжаГЄЗНаЮЕФУцЛ§ЕШгкЖдгІЕФЦЕТЪЃЌЧѓЕУ
ФкЕФЦЕЪ§ЃЌРћгУЙЋЪНЧѓЕУЦЕТЪЃЌЭъГЩЦЕТЪЗжВМБэЃЌЭъЩЦжБЗНЭМЃЌРћгУжБЗНЭМжаГЄЗНаЮЕФУцЛ§ЕШгкЖдгІЕФЦЕТЪЃЌЧѓЕУ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЯШЫуГіЮТВюДѓгкЕШгк![]() ЕФЬьЪ§ЃЌдйевГіЮТВюдкЧјМф
ЕФЬьЪ§ЃЌдйевГіЮТВюдкЧјМф![]() ФкЕФЬьЪ§ЃЌСаГіЫљгаЕФЛљБОЪТМўЃЌдйЪ§ГіТњзуЬѕМўЕФЛљБОЪТМўЪ§ЃЌРћгУИХТЪЙЋЪНЧѓЕУНсЙћ.
ФкЕФЬьЪ§ЃЌСаГіЫљгаЕФЛљБОЪТМўЃЌдйЪ§ГіТњзуЬѕМўЕФЛљБОЪТМўЪ§ЃЌРћгУИХТЪЙЋЪНЧѓЕУНсЙћ.
(Ђё)

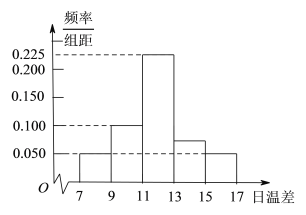
НтЕУ![]() .
.
(Ђђ) вРЬтвтЃЌШеЮТВюдкЧјМф![]() ФкЕФга3ЬьЃЌЩшЮЊ
ФкЕФга3ЬьЃЌЩшЮЊ![]() ЃЛ
ЃЛ
ЦјЮТВюдк![]() ФкЕФга2ЬьЃЌЩшЮЊ
ФкЕФга2ЬьЃЌЩшЮЊ![]() .
.
дђДгШеЮТВюДѓгкЕШгк![]() ЕФет5ЬьРяЫцЛњГщШЁ2ЬьЕФЛљБОЪТМўПеМфЮЊ
ЕФет5ЬьРяЫцЛњГщШЁ2ЬьЕФЛљБОЪТМўПеМфЮЊ
![]() ЦфАќКЌЕФЛљБОЪТМўЪ§
ЦфАќКЌЕФЛљБОЪТМўЪ§![]() .
.
ЩшЪТМў![]() ЁАСНЬьжажСЩйгавЛЬьЕФЮТВюдкЧјМф
ЁАСНЬьжажСЩйгавЛЬьЕФЮТВюдкЧјМф![]() ФкЁБ.
ФкЁБ. ![]() ЃЌ
ЃЌ
ЦфАќКЌЕФЛљБОЪТМўЪ§![]() .
.
дђ![]() .
.
ЫљвдетСНЬьжажСЩйгавЛЬьЕФЮТВюдкЧјМф![]() ФкЕФИХТЪЮЊ
ФкЕФИХТЪЮЊ![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() дк
дк![]() гы
гы![]() ЪБЖМШЁЕУМЋжЕЃЛ
ЪБЖМШЁЕУМЋжЕЃЛ
ЃЈ1ЃЉЧѓ![]() ЕФжЕгыКЏЪ§
ЕФжЕгыКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШєЖд![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓ
КуГЩСЂЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШє![]() КуГЩСЂЃЌЪдШЗЖЈЪЕЪ§
КуГЩСЂЃЌЪдШЗЖЈЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉжЄУїЃК ![]()
![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧЬнаЮABCPжаЃЌCPЁЮABЃЌCPЁЭCBЃЌ![]() ,CP=2ЃЌDЪЧCPЕФжаЕуЃЌНЋЁїPADбиADелЦ№ЃЌЪЙЕУPDЁЭУцABCDЃЎ
,CP=2ЃЌDЪЧCPЕФжаЕуЃЌНЋЁїPADбиADелЦ№ЃЌЪЙЕУPDЁЭУцABCDЃЎ

ЃЈ1ЃЉЧѓжЄЃКЦНУцPADЁЭЦНУцPCDЃЛ
ЃЈ2ЃЉШєEЪЧPCЕФжаЕуЃЌЧѓШ§РтзЖDЉPEBЕФЬхЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтзЖ![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыЦНУц
гыЦНУц![]() ГЩ
ГЩ![]() НЧЃЌ
НЧЃЌ ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ ![]() ЃЌ
ЃЌ ![]() .
.

ЃЈЂёЃЉШє![]() ЃЌЧѓжЄЃКЦНУц
ЃЌЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЯвжЕЕФШЁжЕЗЖЮЇ.
ЫљГЩНЧЕФе§ЯвжЕЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСШчЭМЕФГЬађПђЭМЃЌдЫааЯргІЕФГЬађЃЌдђЪфГіnЕФжЕЮЊЃЈ ЃЉ 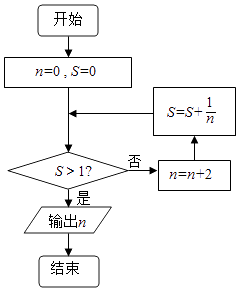
A.6
B.8
C.10
D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
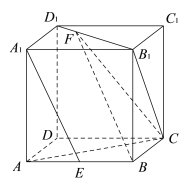
ЁОЬтФПЁПШчЭМЃЌдкРтГЄЮЊ1ЕФе§ЗНЬх![]() жаЃЌ
жаЃЌ ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЖЏЕу.
ЩЯвЛЖЏЕу.
ЃЈЂёЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЕБ![]() ЪБЃЌЧѓШ§РтзЖ
ЪБЃЌЧѓШ§РтзЖ![]() ЕФЬхЛ§ЃЛ
ЕФЬхЛ§ЃЛ
ЃЈЂѓЃЉдкЯпЖЮ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЦНУц
ЦНУц![]() ЃПЫЕУїРэгЩ.
ЃПЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() :
:![]() гыХзЮяЯп
гыХзЮяЯп![]() :
:![]()
ЃЈ1ЃЉШєжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрЧаЃЌЧѓЪЕЪ§
ЯрЧаЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШєжБЯп![]() ОЙ§ХзЮяЯпЕФНЙЕуЃЌЧвгыХзЮяЯпЯрНЛгк
ОЙ§ХзЮяЯпЕФНЙЕуЃЌЧвгыХзЮяЯпЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЕБХзЮяЯпЩЯвЛЖЏЕу
СНЕуЃЌЕБХзЮяЯпЩЯвЛЖЏЕу![]() Дг
Дг![]() ЕН
ЕН![]() дЫЖЏЪБЃЌЧѓ
дЫЖЏЪБЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЁЃ
УцЛ§ЕФзюДѓжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГівдЯТУќЬтЃЌЦфжаецУќЬтЕФИіЪ§ЪЧЃЈ ЃЉ
ЂйШєЁА![]() Лђ
Лђ![]() ЁБЪЧМйУќЬтЃЌдђЁА
ЁБЪЧМйУќЬтЃЌдђЁА![]() Чв
Чв![]() ЁБЪЧецУќЬтЃЛ
ЁБЪЧецУќЬтЃЛ
ЂкУќЬтЁАШє![]() ЃЌдђ
ЃЌдђ![]() Лђ
Лђ![]() ЁБЮЊецУќЬтЃЛ
ЁБЮЊецУќЬтЃЛ
ЂлвбжЊПеМфШЮвтвЛЕу![]() КЭВЛЙВЯпЕФШ§Еу
КЭВЛЙВЯпЕФШ§Еу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЫФЕуЙВУцЃЛ
ЫФЕуЙВУцЃЛ
ЂмжБЯп![]() гыЫЋЧњЯп
гыЫЋЧњЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌШє
СНЕуЃЌШє![]() ЃЌдђетбљЕФжБЯпга3ЬѕЃЛ
ЃЌдђетбљЕФжБЯпга3ЬѕЃЛ
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com