
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 中点,沿直线
中点,沿直线![]() 将
将![]() 翻折成
翻折成![]() ,使平面
,使平面![]() 平面
平面![]() .点
.点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,使
向上翻折,使![]() 与
与![]() 重合,则
重合,则![]() __________,四棱锥
__________,四棱锥![]() 的体积为__________.
的体积为__________.

【答案】2 ![]()
【解析】
过![]() 作
作![]() ,垂足为
,垂足为![]() ,连
,连![]() ,则
,则![]() ,因为平面
,因为平面![]() 平面
平面![]() ,取
,取![]() 的中点
的中点![]() ,连
,连![]() ,因为
,因为![]() ,则
,则![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 三点共线,在三角形
三点共线,在三角形![]() 中,求出
中,求出![]() ,在
,在![]()
![]() 中,求出
中,求出![]() ,在△
,在△![]() 中,
中,![]() ,根据余弦定理求出
,根据余弦定理求出![]() ,在直角△
,在直角△![]() 中,求出
中,求出![]() ,
,![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,在直角△
,在直角△![]() 中,求出
中,求出![]() ,则
,则![]() ,从而可得四边形
,从而可得四边形![]() 的面积为
的面积为![]() ,最后由四棱锥的体积公式可得体积.
,最后由四棱锥的体积公式可得体积.
如图:过![]() 作
作![]() ,垂足为
,垂足为![]() ,连
,连![]() ,则
,则![]() ,
,
因为平面![]() 平面
平面![]() ,取
,取![]() 的中点
的中点![]() ,连
,连![]() ,因为
,因为![]() ,则
,则![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,所以
,所以![]() 三点共线,
三点共线,

在三角形![]() 中,
中,![]() ,所以
,所以![]()
![]() ,所以
,所以![]() ,
,
在![]()
![]() 中,
中,![]() ,所以
,所以![]() ,
,
在△![]() 中,
中,![]()
![]() ,
,
设![]() ,则
,则![]() ,
,
在△![]() 中
中![]() ,
,
所以![]() ,解得
,解得![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,
,
在直角△![]() 中,
中,![]() ,即
,即![]() ,解得
,解得![]() ,
,
即![]() ,
,
在直角△![]() 中,
中,![]()
![]() ,
,
所以 ,
,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,
在直角△![]() 中,
中,![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以四边形![]() 的面积为
的面积为![]() ,
,
所以四棱锥![]() 的体积为
的体积为![]() ,
,
故答案为:(1)2 (2)![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,以上顶点和右焦点为直径端点的圆与直线
,以上顶点和右焦点为直径端点的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)是否存在斜率为2的直线,使得当直线与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,
,![]() 时,能在直线
时,能在直线![]() 上找到一点
上找到一点![]() ,在椭圆
,在椭圆![]() 上找到一点
上找到一点![]() ,满足
,满足![]() ?若存在,求出直线的方程;若不存在,请说明理由.
?若存在,求出直线的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
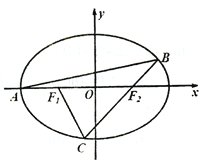
【题目】如图,已知椭圆![]() 的左顶点
的左顶点![]() ,且点
,且点![]() 在椭圆上,
在椭圆上, ![]() 分别是椭圆的左、右焦点。过点
分别是椭圆的左、右焦点。过点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为等腰三角形,求点
为等腰三角形,求点![]() 的坐标;
的坐标;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 折起到
折起到![]() ,使得平面
,使得平面![]() 平面
平面![]() (如图2).
(如图2).

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出
? 若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一幅标准的三角板如图1中,![]() 为直角,
为直角,![]() ,
,![]() 为直角,
为直角,![]() ,且
,且![]() ,把
,把![]() 与
与![]() 拼齐使两块三角板不共面,连结
拼齐使两块三角板不共面,连结![]() 如图2.
如图2.

(1)若![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)在《九章算术》中,称四个面都是直角三角形的三棱锥为“鳖臑”,若图2中![]() ,三棱锥
,三棱锥![]() 的体积为2,则图2是否为鳖臑?说明理由.
的体积为2,则图2是否为鳖臑?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月16日,公安部联合阿里巴巴推出的“钱盾反诈机器人”正式上线,当普通民众接到电信网络诈骗电话,公安部钱盾反诈预警系统预警到这一信息后,钱盾反诈机器人即自动拨打潜在受害人的电话予以提醒,来电信息显示为“公安反诈专号”.某法制自媒体通过自媒体调查民众对这一信息的了解程度,从5000多参与调查者中随机抽取200个样本进行统计,得到如下数据:男性不了解这一信息的有50人,了解这一信息的有80人,女性了解这一信息的有40人.
(1)完成下列![]() 列联表,问:能否在犯错误的概率不超过0.01的前提下,认为200个参与调查者是否了解这一信息与性别有关?
列联表,问:能否在犯错误的概率不超过0.01的前提下,认为200个参与调查者是否了解这一信息与性别有关?
了解 | 不了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(2)该自媒体对200个样本中了解这一信息的调查者按照性别分组,用分层抽样的方法抽取6人,再从这6人中随机抽取3人给予一等奖,另外3人给予二等奖,求一等奖与二等奖获得者都有女性的概率.
附:![]()
P(K2≥k) | 0.01 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义域为R的周期函数,最小正周期为2,且
f(1+x)=f(1-x),当-1≤x≤0时,f(x)=-x.
(1)判断f(x)的奇偶性;
(2)试求出函数f(x)在区间[-1,2]上的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com