
【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求证:![]() ;
;
(3)求证:![]() 有且仅有两个零点.
有且仅有两个零点.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)求出![]() ,即可求出切线的点斜式方程,整理可得切线方程为
,即可求出切线的点斜式方程,整理可得切线方程为![]() ;
;
(2)根据![]() 图像与切线
图像与切线![]() 关系,先证
关系,先证![]() ,再证
,再证![]() ,通过构造函数
,通过构造函数![]() ,
,![]() ,用导数法求出
,用导数法求出![]() 即可;
即可;
(3)对![]() 再求导,可得
再求导,可得![]() 在
在![]() 上单调递增,再由零点存在性定理,可得存在唯一的
上单调递增,再由零点存在性定理,可得存在唯一的![]() ,使得
,使得![]() ,进而求出
,进而求出![]() 的单调区间,再由
的单调区间,再由![]() ,即可证明结论.
,即可证明结论.
(1)![]() ,
,![]() ,
,![]() ,
,
故![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ;
;
(2)先证![]() .令
.令![]() ,
,
![]() ,设
,设![]()
![]() ,故
,故![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() 为
为![]() 的极小值也是最小值,
的极小值也是最小值,
故![]() ,故
,故![]() 成立;
成立;
再证![]() .
.
令![]() ,
,![]() ,
,
令![]() 得
得![]() ,故
,故![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,
上单调递增,![]() 是
是![]() 的极小值也是最小值,
的极小值也是最小值,
故![]() ,故
,故![]() 成立.
成立.
综上知![]() 成立.
成立.
(3)![]() ,
,
设![]()
![]() ,
,
故![]() 在
在![]() 上单调递增,
上单调递增,
因![]() ,
,![]() ,
,
故根据函数零点存在性定理知存在唯一的![]() ,使得
,使得![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
因为![]() ,故在
,故在![]() 上存在一个零点0;且
上存在一个零点0;且![]()
又因为![]() ,
,
故存在唯一![]() 使得
使得![]() ,
,
因此![]() 有且仅有两个零点.
有且仅有两个零点.


科目:高中数学 来源: 题型:
【题目】某市为了改善居民的休闲娱乐活动场所,现有一块矩形![]() 草坪如下图所示,已知:
草坪如下图所示,已知:![]() 米,
米,![]() 米,拟在这块草坪内铺设三条小路
米,拟在这块草坪内铺设三条小路![]() 、
、![]() 和
和![]() ,要求点
,要求点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 时上,且
时上,且![]() .
.
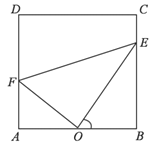
(1)设![]() ,试求
,试求![]() 的周长
的周长![]() 关于
关于![]() 的函数解析式,并求出此函数的定义域;
的函数解析式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为![]() 元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬我国优秀传统文化,某中学广播站在中国传统节日:春节、元宵节、清明节、端午节、中秋节这5个节日中随机选取2个节日来讲解其文化内涵,则春节被选中的概率是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买每满![]() 元的商品即可抽奖一次.抽奖规则如下:抽奖者掷各面标有
元的商品即可抽奖一次.抽奖规则如下:抽奖者掷各面标有![]() 点数的正方体骰子
点数的正方体骰子![]() 次,若掷得点数大于
次,若掷得点数大于![]() ,则可继续在抽奖箱中抽奖;否则获得三等奖,结束抽奖,已知抽奖箱中装有
,则可继续在抽奖箱中抽奖;否则获得三等奖,结束抽奖,已知抽奖箱中装有![]() 个红球与
个红球与![]() 个白球,抽奖者从箱中任意摸出
个白球,抽奖者从箱中任意摸出![]() 个球,若
个球,若![]() 个球均为红球,则获得一等奖,若
个球均为红球,则获得一等奖,若![]() 个球为
个球为![]() 个红球和
个红球和![]() 个白球,则获得二等奖,否则,获得三等奖(抽奖箱中的所有小球,除颜色外均相同).
个白球,则获得二等奖,否则,获得三等奖(抽奖箱中的所有小球,除颜色外均相同).
![]() 若
若![]() ,求顾客参加一次抽奖活动获得三等奖的概率;
,求顾客参加一次抽奖活动获得三等奖的概率;
![]() 若一等奖可获奖金
若一等奖可获奖金![]() 元,二等奖可获奖金
元,二等奖可获奖金![]() 元,三等奖可获奖金
元,三等奖可获奖金![]() 元,记顾客一次抽奖所获得的奖金为
元,记顾客一次抽奖所获得的奖金为![]() ,若商场希望
,若商场希望![]() 的数学期望不超过
的数学期望不超过![]() 元,求
元,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知定点![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点 ,则直线
两点 ,则直线![]() 与
与![]() 斜率之积是否为定值,若是求出定值;若不是请说明理由.
斜率之积是否为定值,若是求出定值;若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设矩阵M=![]() (其中a>0,b>0).
(其中a>0,b>0).
(1)若a=2,b=3,求矩阵M的逆矩阵M-1;
(2)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′:![]() +y2=1,求a,b的值.
+y2=1,求a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com