
【题目】将平面上每个点都以红、蓝两色之一着色,证明:存在这样的两个相似三角形,它们的相似比为1995,并且每一个三角形的三个顶点同色。
【答案】见解析
【解析】
首先证明平面上一定存在三顶点同色的直角三角形.在平面上任作直线![]() ,则
,则![]() 上必有两点同色,设此两点为
上必有两点同色,设此两点为![]() ,
,![]() .过
.过![]() ,
,![]() 分别作
分别作![]() 的垂线
的垂线![]() ,
,![]() .如果
.如果![]() 或
或![]() 上有与
上有与![]() ,
,![]() 同色的点
同色的点![]() ,则
,则
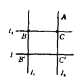
![]() 即为三顶点同色的直角三角形.如果
即为三顶点同色的直角三角形.如果![]() 与
与![]() 上除
上除![]() 与
与![]() 外其余点均与
外其余点均与![]() ,
,![]() 异色,则在
异色,则在![]() 上取异于
上取异于![]() 的两点
的两点![]() ,
,![]() ,并过
,并过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 即为三顶点同色的直角三角形.因此,平面上一定存在三顶点同色的直角三角形,设其中之一为
即为三顶点同色的直角三角形.因此,平面上一定存在三顶点同色的直角三角形,设其中之一为![]() .将
.将![]() 对称地补成矩形
对称地补成矩形![]() .用两组分别平行于
.用两组分别平行于![]() 与
与![]() 的
的![]() 等分平行线将矩形
等分平行线将矩形![]() 等分成
等分成![]() 个与原矩形相似的小矩形.(如图)
个与原矩形相似的小矩形.(如图)
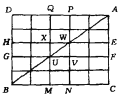
以下用反证法证明:若![]() 为奇数,则在这些小矩形中必有一个,它的顶点中至少有三个同色,即存在一个三顶点同色的小直角三角形.假设不存在三顶点同色的小直角三角形.线段
为奇数,则在这些小矩形中必有一个,它的顶点中至少有三个同色,即存在一个三顶点同色的小直角三角形.假设不存在三顶点同色的小直角三角形.线段![]() 上端点及分点共
上端点及分点共![]() 个,
个,![]() 为偶数,因此
为偶数,因此![]() 上必有相邻的两点同色(若每相邻两点异色,则
上必有相邻的两点同色(若每相邻两点异色,则![]() ,
,![]() 亦应异色,与已知矛盾),不妨设为
亦应异色,与已知矛盾),不妨设为![]() ,
,![]() .则
.则![]() ,
,![]() 所在的小矩形的另两个顶点必与
所在的小矩形的另两个顶点必与![]() ,
,![]() 异色(否则已出现同色小三角形).依次类推,可知矩形
异色(否则已出现同色小三角形).依次类推,可知矩形![]() 中,每条竖线上的两顶点都同色.同理,线段
中,每条竖线上的两顶点都同色.同理,线段![]() 上有相邻两点
上有相邻两点![]() ,
,![]() 同色,也有矩形
同色,也有矩形![]() ,其中每条横线上的两顶点都同色.设矩形
,其中每条横线上的两顶点都同色.设矩形![]() 与
与![]() 的公共部分为小矩形
的公共部分为小矩形![]() ,由以上所说,
,由以上所说,![]() 与
与![]() 同色且
同色且![]() 与
与![]() 同色,从而
同色,从而![]() 即是三顶点同色的小直角三角形.这与假设矛盾.因此必存在一个三顶点同色的小直角三角形.这个三顶点同色的小直角三角形与原直角三角形是相似的,相似比为
即是三顶点同色的小直角三角形.这与假设矛盾.因此必存在一个三顶点同色的小直角三角形.这个三顶点同色的小直角三角形与原直角三角形是相似的,相似比为![]() ,当
,当![]() 时就是题目所要证明的结论.
时就是题目所要证明的结论.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利,根据大数据统计,某条地铁线路运行时,发车时间间隔![]() (单位:分钟)满足:
(单位:分钟)满足: ![]() ,平均每班地铁的载客人数
,平均每班地铁的载客人数![]() (单位:人)与发车时间间隔
(单位:人)与发车时间间隔![]() 近似地满足函数关系:
近似地满足函数关系: ,
,
(1)若平均每班地铁的载客人数不超过1560人,试求发车时间间隔![]() 的取值范围;
的取值范围;
(2)若平均每班地铁每分钟的净收益为![]() (单位:元),则当发车时间间隔
(单位:元),则当发车时间间隔![]() 为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
为多少时,平均每班地铁每分钟的净收益最大?并求出最大净收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一学生有1000名学生参加一次数学小测验,随机抽取200名学生的测验成绩得如图所示的频率分布直方图:

(1)求该学校高一学生随机抽取的200名学生的数学平均成绩![]() 和标准差
和标准差![]() (同一组中的数据用该组区间的中点值做代表);
(同一组中的数据用该组区间的中点值做代表);
(2)试估计该校高一学生在这一次的数学测验成绩在区间![]() 之内的概率是多少?测验成绩在区间
之内的概率是多少?测验成绩在区间![]() 之外有多少位学生?(参考数据:
之外有多少位学生?(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果农从经过筛选(每个水果的大小最小不低于50克,最大不超过100克)的10000个水果中抽取出100个样本进行统计,得到如下频率分布表:
级别 | 大小(克) | 频数 | 频率 |
一级果 |
| 5 | 0.05 |
二级果 |
|
| |
三级果 |
| 35 |
|
四级果 |
| 30 | |
五级果 |
| 20 | |
合计 | 100 |
请根据频率分布表中所提供的数据,解得下列问题:
(1)求![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)若从四级果,五级果中按分层抽样的方法抽取5个水果,并从中选出2个作为展品,求2个展品中仅有1个是四级果的概率;
(3)若将水果作分级销售,预计销售的价格![]() 元/个与每个水果的大小
元/个与每个水果的大小![]() 克关系是:
克关系是: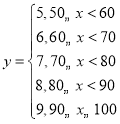 ,则预计10000个水果可收入多少元?
,则预计10000个水果可收入多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】榆林市政府坚持保护环境和节约资源,坚持推进生态文明建设。若市财政局下拨专款100百万元,分别用于植绿护绿和处理污染两个生态维护项目,植绿护绿项目五年内带来的生态收益可表示为投放资金![]() (单位:百万元)的函数
(单位:百万元)的函数![]() (单位:百万元):
(单位:百万元):![]() ,处理污染项目五年内带来的生态收益可表示为投放资金
,处理污染项目五年内带来的生态收益可表示为投放资金![]() 单位:(单位:百万元)的函数
单位:(单位:百万元)的函数![]() (单位:百万元):
(单位:百万元):![]() 。
。
(1)设分配给植绿护绿项目的资金为![]() (百万元),则两个生态项目五年内带来的收益总和为y,写出y关于
(百万元),则两个生态项目五年内带来的收益总和为y,写出y关于![]() 的函数解析式和定义域;
的函数解析式和定义域;
(2)试求出y的最大值,并求出此时对两个生态项目的投资分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(a,0)、B(0,b)(其中ab≠0)O为坐标原点.
(1)动点P(x,y)满足![]() ,求P点的轨迹方程;
,求P点的轨迹方程;
(2)设![]() 是线段AB的n+1(n≥1)等分点,当n=2018时,求
是线段AB的n+1(n≥1)等分点,当n=2018时,求![]() 的值;
的值;
(3)若a=b=1,t∈[0,1],求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定![]() ,
,![]() ,
,![]() ,
,![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,
,![]() ,在
,在![]() 所在平面作直线
所在平面作直线![]() 与
与![]() 的某两边相交,沿
的某两边相交,沿![]() 将
将![]() 折成一个空间图形,将由
折成一个空间图形,将由![]() 分成的小三角形的不在
分成的小三角形的不在![]() 上的顶点与另一部分的顶点连接,形成一个三棱锥或四棱锥。问:
上的顶点与另一部分的顶点连接,形成一个三棱锥或四棱锥。问:
(1)当![]() 时,
时,![]() 如何作,并折成何种锥体,才能使所得锥体体积最大?(需详证)
如何作,并折成何种锥体,才能使所得锥体体积最大?(需详证)
(2)当![]() 时,
时,![]() 如何作,并折成何种锥体,才能使所得锥体体积最大?(叙述结果,不要证明)
如何作,并折成何种锥体,才能使所得锥体体积最大?(叙述结果,不要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com