【题目】已知函数f（x）= 
+log2x．
（1）求f（2），f（ 
），f（4），f（ 
）的值，并计算f（2）+f（ ），f（4）+f（ ）；
（2）求f（1）+f（2）+f（3）+…+f（2016）+f（ ）+f（ 
）+…f（ 
）的值．
【答案】
（1）解：∵f（x）= 
+log2x，
∴f（2）= 
= 
，
f（ 
）= 
，
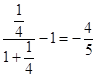f（4）=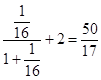 
，
f（ 
）= 
，
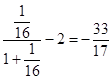∴f（2）+f（ ）=1，f（4）+f（ ）=1
（2）解：∵f（x）+f（ 
）= + 
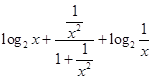=1，
∴f（1）+f（2）+f（3）+…+f（2016）+f（ ）+f（ 
）+…f（ 
）
=f（1）+[f（2）+f（ ）]+[f（3）+f（ ）]+…+[f（2016）+f（ ）]
= 
= 
【解析】（1）由f（x）= +log2x，能求出f（2），f（ ），f（4），f（ ），f（2）+f（ ），f（4）+f（ ）的值．（2）由f（x）+f（ ）=1，能求出f（1）+f（2）+f（3）+…+f（2016）+f（ ）+f（ ）+…f（ ）的值．
【考点精析】解答此题的关键在于理解函数的值的相关知识，掌握函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
（x∈R）
（1）用定义证明f（x）是增函数；
（2）若g（x）=f（x）﹣a是奇函数，求g（x）在（﹣∞，a]上的取值集合．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）
某学校简单随机抽样方法抽取了100名同学，对其日均课外阅读时间：（单位：分钟）进行调查，结果如下：
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”
（1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？
（2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动．
①求抽取的4为同学中有男同学又有女同学的概率；
②记抽取的“读书迷”中男生人数为X，求X的分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
在
单调递增，其中
．
（1）求
的值；
（2）若
，当
时，试比较
与
的大小关系（其中
是
的导函数），请写出详细的推理过程；
（3）当
时， 
恒成立，求
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）=2+log3x，x∈[1，9]，g（x）=[f（x）]2+f（x2），
（1）求g（x）的定义域；
（2）求g（x）的最大值以及g（x）取最大值时x的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）= 
（ax﹣a﹣x）（a＞0且a≠1）．
（1）判断f（x）的奇偶性．
（2）讨论f（x）的单调性．
（3）当x∈[﹣1，1]时，f（x）≥b恒成立，求b的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=ln 
．
（1）求函数f（x）的定义域，并判断函数f（x）的奇偶性；
（2）对于x∈[2，6]，f（x）＞ln 
恒成立，求实数m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
