

 .
. ,其中
,其中 为第
为第 组数据的频率,
组数据的频率, 是第
是第 组数据的中间值.各组的频率等于小矩形的面积,由此求出各组数据的频率代入以上公式即得平均数.
组数据的中间值.各组的频率等于小矩形的面积,由此求出各组数据的频率代入以上公式即得平均数.  ,再根据频率求得50~60分数段的人数为40×0.1=4人.将第一组和第五组的同学编号,然后一一列举出所有可能结果. 两人成绩差大于20,则这两人分别来自第一组和第五组,数出其中的个数,利用古典概型概率公式便得所求概率.
,再根据频率求得50~60分数段的人数为40×0.1=4人.将第一组和第五组的同学编号,然后一一列举出所有可能结果. 两人成绩差大于20,则这两人分别来自第一组和第五组,数出其中的个数,利用古典概型概率公式便得所求概率. =40人, 5分
=40人, 5分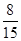 12分
12分

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题


| A.800! | B.810! | C.811! | D.812! |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.90 | B.75 | C.60 | D.45 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
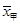 ,
,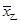 ,则下列说法正确的是( )
,则下列说法正确的是( )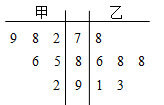
A. ,乙比甲成绩稳定,应该选乙参加比赛 ,乙比甲成绩稳定,应该选乙参加比赛 |
B. ,甲比乙成绩稳定,应该选甲参加比赛 ,甲比乙成绩稳定,应该选甲参加比赛 |
C.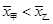 ,甲比乙成绩稳定,应该选甲参加比赛 ,甲比乙成绩稳定,应该选甲参加比赛 |
D.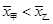 ,乙比甲成绩稳定,应该选乙参加比赛 ,乙比甲成绩稳定,应该选乙参加比赛 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com