
【题目】已知函数f(x)=2sin2( ![]() +x)﹣
+x)﹣ ![]() cos2x,
cos2x,
(1)求f(x)的最小正周期及单调递减区间;
(2)当x ![]() 时,求f(x)的最大值和最小值.
时,求f(x)的最大值和最小值.
【答案】
(1)解:∵f(x)=[1﹣cos( ![]() +2x)]﹣
+2x)]﹣ ![]() cos2x
cos2x
=1+sin2x﹣ ![]() cos2x
cos2x
=1+2sin(2x﹣ ![]() )
)
∴最小正周期T=π
由 ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈Z
+2kπ,k∈Z
得 ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z
+kπ,k∈Z
∴单调递减区间为[ ![]() +kπ,
+kπ, ![]() +kπ]k∈Z
+kπ]k∈Z
(2)解:∵x∈[ ![]() ,
, ![]() ],
],
∴ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() ,
,
即2≤1+2sin(2x﹣ ![]() )≤3,
)≤3,
∴f(x)max=3,f(x)min=2.
【解析】(1)由两角和与差的正弦函数将f(x)=[1﹣cos( ![]() +2x)]﹣
+2x)]﹣ ![]() cos2x化为f(x)=1+2sin(2x﹣
cos2x化为f(x)=1+2sin(2x﹣ ![]() ),利用正弦函数的性质即可求f(x)的最小正周期及单调递减区间;(2)由x∈[
),利用正弦函数的性质即可求f(x)的最小正周期及单调递减区间;(2)由x∈[ ![]() ,
, ![]() ],可求得2x﹣
],可求得2x﹣ ![]() 的范围,从而可得f(x)的最大值和最小值.
的范围,从而可得f(x)的最大值和最小值.
【考点精析】本题主要考查了两角和与差的正弦公式和二倍角的余弦公式的相关知识点,需要掌握两角和与差的正弦公式:![]() ;二倍角的余弦公式:
;二倍角的余弦公式:![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】自2016年下半年起六安市区商品房价不断上涨,为了调查研究六安城区居民对六安商品房价格承受情况,寒假期间小明在六安市区不同小区分别对50户居民家庭进行了抽查,并统计出这50户家庭对商品房的承受价格(单位:元/平方),将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组(单位:元/平方),并作出频率分布直方图如图:
五组(单位:元/平方),并作出频率分布直方图如图:
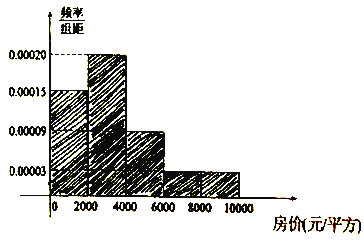
(Ⅰ)试根据频率分布直方图估计出这50户家庭对商品房的承受价格平均值(单位:元/平方);
(Ⅱ)为了作进一步调查研究,小明准备从承受能力超过4000元/平方的居民中随机抽出2户进行再调查,设抽出承受能力超过8000元/平方的居民为![]() 户,求
户,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a,b,c分别是角A,B,C的对边,且a=80,b=100,A= ![]() ,则此三角形是( )
,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角或钝角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A′B′C′D′. 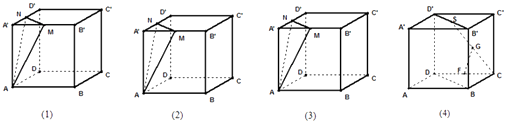
(1)设M,N分别是A′D′,A′B′的中点,试在下列三个正方体中各作出一个过正方体顶点且与平面AMN平行的平面(不用写过程)
(2)设S是B′D′的中点,F,G分别是DC,SC的中点,求证:直线GF∥平面BDD′B′.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点为极点,
),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)讨论直线![]() 与圆
与圆![]() 的公共点个数;
的公共点个数;
(Ⅱ)过极点作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求点
,求点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长.
相交所得弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2+bx+c.
(1)若f(﹣1)=0,f(0)=0,求出函数f(x)的零点;
(2)若f(x)同时满足下列条件:①当x=﹣1时,函数f(x)有最小值0,②f(1)=1求函数f(x)的解析式;
(3)若f(1)≠f(3),证明方程f(x)= ![]() [f(1)+f(3)]必有一个实数根属于区间(1,3)
[f(1)+f(3)]必有一个实数根属于区间(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
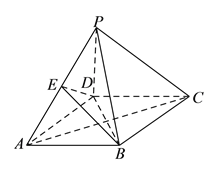
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 的交点记为
的交点记为![]() ,求证
,求证![]() 平面
平面![]() ;
;
(3)在(2)的条件下求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
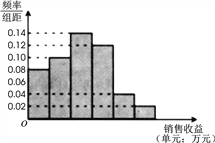
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.
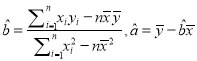
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com