
(1)如图,对于任一给定的四面体![]() ,找出依次排列的四个相互平行的平面
,找出依次排列的四个相互平行的平面![]() ,使得
,使得![]() ,且其中每相邻两个平面间的距离都相等;
,且其中每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面![]() ,其中每相邻两个平面间的距离都为1,若一个正四面体
,其中每相邻两个平面间的距离都为1,若一个正四面体![]() 的四个顶点满足
的四个顶点满足![]() ,求该正四面体
,求该正四面体![]() 的体积.
的体积.
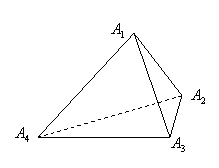
【解析】
(1)如图所示,取![]() 的三等分点
的三等分点![]() ,
,![]() ,
,![]() 的中点
的中点![]() ,
,
![]() 的中点
的中点![]() ,过三点
,过三点![]() ,
,![]() ,
,![]() 作平面
作平面![]() ,过三点
,过三点![]() ,
,![]() ,
,![]() 作平面
作平面![]() ,因为
,因为![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() ,再过点
,再过点![]() ,
,![]() 分别作平面
分别作平面![]() ,
,![]() 与平面
与平面![]() 平行,那么四个平面
平行,那么四个平面![]() ,
,![]() ,
,![]() ,
,![]() 依次相互平行,由线段
依次相互平行,由线段![]() 被平行平面
被平行平面![]() ,
,![]() ,
,![]() ,
,![]() 截得的线段相等知,期中每相邻两个平面间的距离相等,故
截得的线段相等知,期中每相邻两个平面间的距离相等,故![]() ,
,![]() ,
,![]() ,
,![]() 为所求平面.
为所求平面.
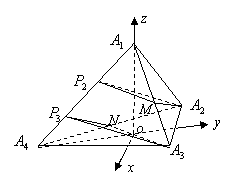
(2)解法一:当(1)中的四面体为正四面体,若所得的四个平行平面,每相邻两平面之间的距离为1,则正四面体![]() 就是满足题意的正四面体.设正四面体的棱长为
就是满足题意的正四面体.设正四面体的棱长为![]() ,以
,以![]() 的中心
的中心![]() 为坐标原点,以直线
为坐标原点,以直线![]() 为
为![]() 轴,直线
轴,直线![]() 为
为![]() 轴建立如图的右手直角坐标系,
轴建立如图的右手直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]()
令![]() ,
,![]() 为
为![]() 的三等分点,
的三等分点,![]() 为
为![]() 的中点,有
的中点,有
![]() ,
,![]() ,所以
,所以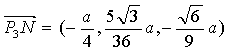 ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,有
,有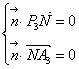 ,即
,即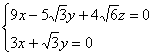
所以,![]() .因为
.因为![]() ,
,![]() ,
,![]() ,
,![]() 相邻平面之间的距离为1,所以点
相邻平面之间的距离为1,所以点![]() 到平面
到平面![]() 的距离
的距离
 ,解得
,解得![]()
由此可得,边长为![]() 的正四面体
的正四面体![]() 满足条件.
满足条件.
所以所求正四面体的体积![]() .
.
解法二:如图,现将此正四面体![]() 置于一个正方体
置于一个正方体![]() 中,(或者说,在正四面体的四个面外侧各镶嵌一个直角正三棱锥,得到一个正方体),
中,(或者说,在正四面体的四个面外侧各镶嵌一个直角正三棱锥,得到一个正方体),
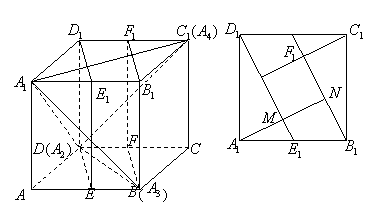
![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 和
和![]() 是两个平行平面,若其距离为1,则正四面体
是两个平行平面,若其距离为1,则正四面体![]() 即为满足条件的正四面体.右图是正方体的上底面,现设正方体的棱长为
即为满足条件的正四面体.右图是正方体的上底面,现设正方体的棱长为![]() ,若
,若![]() ,则有
,则有![]() ,
,![]()
据![]() ,得
,得![]() ,
,
于是正四面体的棱长![]() ,其体积
,其体积![]() .
.
(即等于一个棱长为![]() 的正方体割去四个直角正三棱锥后的体积)
的正方体割去四个直角正三棱锥后的体积)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 (1)如图,对于任一给定的四面体A1A2A3A4,找出依次排列的四个相互平行的α1,α2,α3,α4,使得Ai∈αi(i=1,2,3,4),且其中每相邻两个平面间的距离都相等;
(1)如图,对于任一给定的四面体A1A2A3A4,找出依次排列的四个相互平行的α1,α2,α3,α4,使得Ai∈αi(i=1,2,3,4),且其中每相邻两个平面间的距离都相等;查看答案和解析>>
科目:高中数学 来源:2011年江西省普通高中招生考试理科数学 题型:解答题
(本小题满分14分)
(1)如图,对于任一给定的四面体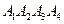 ,找出依
,找出依
次排列的四个相互平行的平面 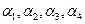 ,使
,使
得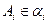 (i=1,2,3,4),且其中每相邻两个平面间
(i=1,2,3,4),且其中每相邻两个平面间
的距离都相等;
(2)给定依次排列的四个相互平行的平面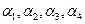 ,其中每相邻两个平面间的距离为1,若一个正四面体
,其中每相邻两个平面间的距离为1,若一个正四面体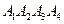 的四个顶点满足:
的四个顶点满足: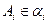 (i=1,2,3,4),求该正四面体
(i=1,2,3,4),求该正四面体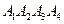 的体积.
的体积.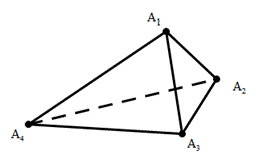
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)如图,对于任一给定的四面体![]() ,找出依次排列的四个相互平行的平面
,找出依次排列的四个相互平行的平面![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,且其中每相邻两个平面间的距离都相等;
,且其中每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面![]() ,
,![]() ,
,![]() ,
,![]() ,其中每相邻两个平面间的距离都为1,若一个正四面体
,其中每相邻两个平面间的距离都为1,若一个正四面体![]() 的四个顶点满足:
的四个顶点满足:![]() ,求该正四面体
,求该正四面体![]() 的体积.
的体积.
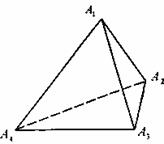
查看答案和解析>>
科目:高中数学 来源:2011年高考试题数学理(江西卷)解析版 题型:解答题
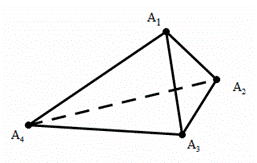
(1)如图,对于任一给定的四面体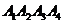 ,找出依
,找出依
次排列的四个相互平行的平面 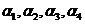 ,使
,使
得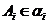 (i=1,2,3,4),且其中每相邻两个平面间
(i=1,2,3,4),且其中每相邻两个平面间
的距离都相等;
(2)给定依次排列的四个相互平行的平面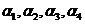 ,其中每相邻两个平面间的距离为1,若一个正四面体
,其中每相邻两个平面间的距离为1,若一个正四面体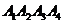 的四个顶点满足:
的四个顶点满足: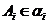 (i=1,2,3,4),求该正四面体
(i=1,2,3,4),求该正四面体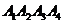 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com