
数列 的前
的前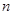 项和为
项和为 ,
,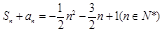 .
.
(Ⅰ)设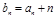 ,证明:数列
,证明:数列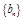 是等比数列;
是等比数列;
(Ⅱ)求数列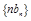 的前
的前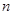 项和
项和 .
.
(Ⅲ)若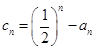 ,
,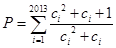 ,求不超过
,求不超过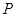 的最大的整数值.
的最大的整数值.
(Ⅰ)详见解析;(Ⅱ)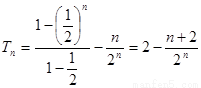 ;(Ⅲ)
;(Ⅲ)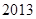 。
。
【解析】
试题分析:(Ⅰ)利用递推式相减后,构造等比数列进行证明;(Ⅱ)利用错位相减法求解;(Ⅲ)借助第一问的结论,确定数列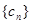 的通项公式,进而采用裂项相消法求解P,进而利用放缩求不超过
的通项公式,进而采用裂项相消法求解P,进而利用放缩求不超过 的最大的整数值.
的最大的整数值.
试题解析:(Ⅰ)因为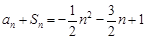 ,
,
所以 ①
当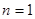 时,
时,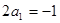 ,则
,则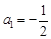 ,
1分
,
1分
② 当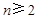 时,
时,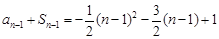 , 2分
, 2分
所以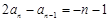 ,即
,即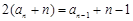 ,
,
所以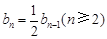 ,而
,而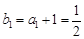 , 3分
, 3分
所以数列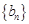 是首项为
是首项为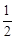 ,公比为
,公比为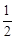 的等比数列,所以
的等比数列,所以 . 4分
. 4分
(Ⅱ)由(Ⅰ)得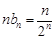 .
.
所以 ①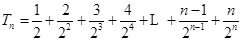 ,
,
②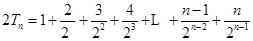 , 6分
, 6分
②-①得: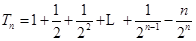 , 7分
, 7分
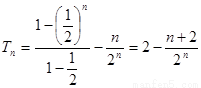 . 9分
. 9分
(Ⅲ)由(1)知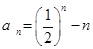
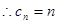 10分
10分
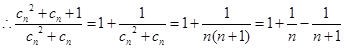 , 12分
, 12分
所以
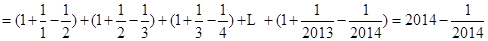 ,
,
故不超过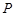 的最大整数为
的最大整数为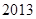 .
13分
.
13分
考点:1.等比数列的证明;2.数列求和。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a4 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| S3 |
| 1 |
| Sn |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,公差
,公差![]()
![]() 成等比数列.
成等比数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若从数列![]() 中依次取出第2项、第4项、第8项,……,
中依次取出第2项、第4项、第8项,……,![]() ,……,按原来顺序组成一个新数列
,……,按原来顺序组成一个新数列![]() ,记该数列的前
,记该数列的前![]() 项和为
项和为![]() ,求
,求![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源:2011届北京市东城区示范校高三第二学期综合练习数学文卷 题型:解答题
(本小题14分)已知数列 为等差数列,
为等差数列, ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
(1)求 、
、 的通项公式;
的通项公式;
(2)若 ,
, 的前
的前 项和为
项和为 ,求
,求 ;
;
(3)试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011年湖南省浏阳一中高二上学期第一次质检数学理卷 题型:解答题
(本小题14分)
数列 的前
的前 项和为
项和为 ,且对
,且对 都有
都有 ,则:
,则:
(1)求数列 的前三项
的前三项 ;
;
(2)根据 上述结果,归纳猜想数列
上述结果,归纳猜想数列 的通项
的通项 公式,并用数学归纳法加以证明.
公式,并用数学归纳法加以证明.
(3)求证:对任意 都有
都有 .
.
查看答案和解析>>
科目:高中数学 来源:2014届广东佛山南海普通高中高三8月质量检测文科数学试卷(解析版) 题型:解答题
数列 的前
的前 项和为
项和为 ,且
,且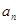 是
是 和
和 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,证明:
,证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com