
【题目】如图所示的程序框图的算法思路源于我国古代数学中的秦九韶算法,执行该程序框图,则输出的结果S表示的值为( ) 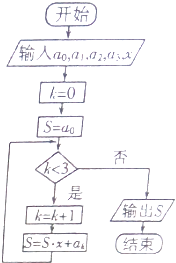
A.a0+a1+a2+a3
B.(a0+a1+a2+a3)x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
【答案】D
【解析】解:当k=0,S=a0时,满足进行循环的条件,执行循环体后,k=1,S=a0x+a1 ,
当k=1,S=a0x+a1时,满足进行循环的条件,执行循环体后,k=2,S=a0x2+a1x+a2 ,
当k=2,S=a0x2+a1x+a2时,满足进行循环的条件,执行循环体后,k=3,S=a0x3+a1x2+a2x+a3 ,
当k=3,S=a0x3+a1x2+a2x+a3时,不满足进行循环的条件,
故输出结果为:a0x3+a1x2+a2x+a3 ,
故选:D
【考点精析】利用程序框图对题目进行判断即可得到答案,需要熟知程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若点![]() 是
是![]() 上的动点,过点
上的动点,过点![]() 作抛物线
作抛物线![]() :
:![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别如下图所示。
甲 | 0 | 1 | 0 | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
乙 | 2 | 3 | 1 | 1 | 0 | 2 | 1 | 1 | 0 | 1 |
从数据上看, ________________机床的性能较好(填“甲”或者“乙”).
查看答案和解析>>
科目:高中数学 来源: 题型:
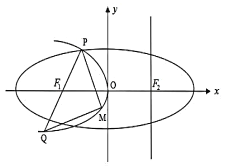
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() 为
为![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交
并延长其交![]() 于点
于点![]() ,
, ![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC= ![]() AB=
AB= ![]() ,平面PBC⊥平面ABCD.
,平面PBC⊥平面ABCD. 
(1)求证:AC⊥PB;
(2)若PB=PC= ![]() ,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为
,问在侧棱PB上是否存在一点M,使得二面角M﹣AD﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
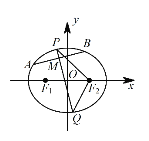
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() (
(![]() ,
,![]() )与椭圆C交于两点A、B,点D满足
)与椭圆C交于两点A、B,点D满足![]() ,经过点D及点
,经过点D及点![]() 的直线的斜率为
的直线的斜率为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 袋中有形状、大小、质地完全一样的![]() 个红球和
个红球和![]() 个白球,从中随机抽出一个球,一定是红球
个白球,从中随机抽出一个球,一定是红球
B. 天气预报“明天降水概率![]() ”,是指明天有
”,是指明天有![]() 的时间会下雨
的时间会下雨
C. 某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票![]() 张,一定会中奖
张,一定会中奖
D. 连续掷一枚均匀硬币,若![]() 次都是正面朝上,则第六次仍然可能正面朝上
次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com