
 的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式
的所有正实数a,如果满足不等式|x-a|<b的一切实数x,也满足不等式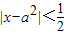 ,求实数b的取值范围.
,求实数b的取值范围. ≤a-b,且 a+b≤a2+
≤a-b,且 a+b≤a2+ ,0<a≤
,0<a≤ .由此可得b小于或等于-a2+a+
.由此可得b小于或等于-a2+a+ 的最小值,且b小于或等于 a2-a+
的最小值,且b小于或等于 a2-a+ 的最小值,由此求得实数b的取值范围.
的最小值,由此求得实数b的取值范围.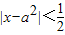 可得,-
可得,- <x-a2<
<x-a2< ,即 a2-
,即 a2- <x<a2+
<x<a2+ .
. ≤a-b,且 a+b≤a2+
≤a-b,且 a+b≤a2+ ,0<a≤
,0<a≤ .
. ,且b≤a2-a+
,且b≤a2-a+ .
. =-
=-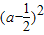 +
+ ∈[
∈[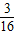 ,
, ],故 b≤
],故 b≤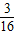 .
.  =
= +
+ ∈[
∈[ ,
,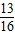 ].故 b≤
].故 b≤ .
. .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源:高考零距离 二轮冲刺优化讲练 数学 题型:044
设对于不大于![]() 的所有正实数a,如果满足不等式|x一a|<b的一切实数x,亦满足不等式|x-a2|<
的所有正实数a,如果满足不等式|x一a|<b的一切实数x,亦满足不等式|x-a2|<![]() ,求实数b的取值范围.
,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com