Question

【题目】已知向量 ， 满足| |=| =1，且|k + |= | ﹣k |（k＞0），令f（k）= ． （Ⅰ）求f（k）= （用k表示）；
（Ⅱ）若f（k）≥x2﹣2tx﹣ 对任意k＞0，任意t∈[﹣1，1]恒成立，求实数x的取值范围．

Answer 1

【答案】解：（Ⅰ）由题设得 ，对 两边平方得：

；

∴ ；

∴ ；

∴ ；

（Ⅱ） ，当且仅当k=1时取“=”；

∵f（k）≥x2﹣2tx﹣ 对任意的k＞0，t∈[﹣1，1]恒成立；

∴ ≥x2﹣2tx﹣ ；

即g（t）=2xt﹣x2+1≥0在[﹣1，1]上恒成立，而g（t）在[﹣1，1]上为单调函数或常函数；

；

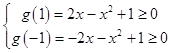解得1﹣ ≤x≤ ﹣1；

故实数x的取值范围为[1﹣ ， ﹣1]．

【解析】（Ⅰ）根据 ，对 两边平方即可求出 的值，从而得出 ；（Ⅱ）先根据基本不等式求出k=1时，f（k）取最小值 ，这样根据条件即可得到 对任意的t∈[﹣1，1]恒成立，即得到g（t）=2xt﹣x2+1≥0对任意的t∈[﹣1，1]恒成立，从而得到 ，这样即可解出x的取值范围．