
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c,cos2C+2 ![]() cosC+2=0.
cosC+2=0.
(1)求角C的大小;
(2)若b= ![]() a,△ABC的面积为
a,△ABC的面积为 ![]() sinAsinB,求sinA及c的值.
sinAsinB,求sinA及c的值.
【答案】
(1)解:∵cos2C+2 ![]() cosC+2=0.
cosC+2=0.
∴2cos2C+2 ![]() cosC+1=0,
cosC+1=0,
即( ![]() cosC+1)2=0,
cosC+1)2=0,
∴cosC=﹣ ![]()
∵0<∠C<π,
∴∠C= ![]() .
.
(2)解:∵c2=a2+b2﹣2abcosC=3a2+2a2=5a2,
∴c= ![]() a,
a,
∴sinC= ![]() sinA,
sinA,
∴sinA= ![]() sinC=
sinC= ![]() ,
,
∵S△ABC= ![]() absinC=
absinC= ![]() sinAsinB,
sinAsinB,
∴ ![]() absinC=
absinC= ![]() sinAsinB,
sinAsinB,
∴ ![]()
![]() sinC=(
sinC=( ![]() )2sinC=
)2sinC= ![]() ,
,
∴c= ![]() =1
=1
【解析】(1)利用正弦定理和已知等式,化简可求得cosC的值,进而求C.(2)利用余弦定理可求得c与a的关系,进而求得sinC,然后利用三角形面积公式和已知等式求得c.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2,∠BAD=60°,M为DC的中点,若N为菱形内任意一点(含边界),则 ![]() 的最大值为( )
的最大值为( ) 
A.3
B.2 ![]()
C.6
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
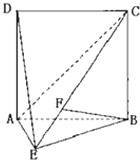
【题目】如图,直二面角![]() 中,四边形ABCD是边长为2的正方形,
中,四边形ABCD是边长为2的正方形,![]() ,F为CE上的点,且
,F为CE上的点,且![]() 平面ACE.
平面ACE.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BCE;
平面BCE;
![]() Ⅱ
Ⅱ![]() 求二面角
求二面角![]() 的余弦值;
的余弦值;
![]() Ⅲ
Ⅲ![]() 求点D到平面ACE的距离.
求点D到平面ACE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=n2+2n;数列{bn}是公比大于1的等比数列,且满足b1+b4=9,b2b3=8.
(Ⅰ)分别求数列{an},{bn}的通项公式;
(Ⅱ)若cn=(﹣1)nSn+anbn , 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于 60分 | 60分 到79分 | 80分 到89分 | 不低 于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
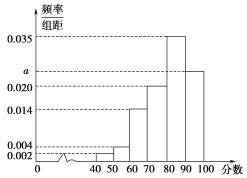
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)在等级为不满意市民中,老年人占![]() ,中青年占
,中青年占![]() ,现从该等级市民中按年龄分层抽取
,现从该等级市民中按年龄分层抽取![]() 人了解不满意的原因,并从中选取
人了解不满意的原因,并从中选取![]() 人担任整改督导员,求至少有一位老年督导员的概率;
人担任整改督导员,求至少有一位老年督导员的概率;
(3)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
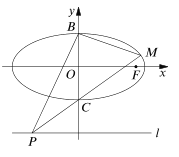
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,点
的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴的交点除外),直线
轴的交点除外),直线![]() 交椭圆于另一个点
交椭圆于另一个点![]() .
.
(1)当直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 时,求
时,求![]() 的面积;
的面积;
(2)①记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
②求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列A:a1,a2,a3,…,定义A的“差数列” ![]() A:
A:![]() ,…
,…
(I)若数列A:a1,a2,a3,…的通项公式![]() ,写出
,写出![]() A的前3项;
A的前3项;
(II)试给出一个数列A:a1,a2,a3,…,使得![]() A是等差数列;
A是等差数列;
(III)若数列A:a1,a2,a3,…的差数列的差数列 ![]() (
(![]() A)的所有项都等于1,且
A)的所有项都等于1,且![]() =
=![]() =0,求
=0,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com