
(本小题满分14分)已知函数
(I)求函数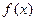 在
在
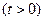 上的最小值;
上的最小值;
(II)对一切 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(III)求证:对一切 ,都有
,都有
(I)f ′(x)=lnx+1,当x∈(0,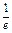 ),f ′(x)<0,f (x)单调递减,
),f ′(x)<0,f (x)单调递减,
当x∈(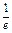 ,+∞),f ′(x)>0,f (x)单调递增. ……2分
,+∞),f ′(x)>0,f (x)单调递增. ……2分
①0<t<t+2<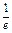 ,t无解;
,t无解;
②0<t<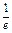 <t+2,即0<t<
<t+2,即0<t<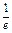 时,f (x)min=f (
时,f (x)min=f (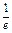 )=-
)=-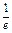 ;
;
③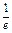 ≤t<t+2,即t≥
≤t<t+2,即t≥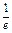 时,f (x)在[t,t+2]上单调递增,f (x)min=f (t)=tlnt;
时,f (x)在[t,t+2]上单调递增,f (x)min=f (t)=tlnt;
所以f (x)min=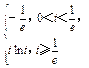 . ……5分
. ……5分
(II)2xlnx≥-x2+ax-3,则a≤2lnx+x+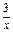 , ……6分
, ……6分
设h (x)=2lnx+x+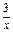 (x>0),则h′(x)=
(x>0),则h′(x)=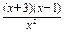 ,x∈(0,1),h′(x)<0,h (x)单调递减,
,x∈(0,1),h′(x)<0,h (x)单调递减,
x∈(1,+∞),h′(x)>0,h (x)单调递增,所以h (x)min=h (1)=4,
(x)单调递增,所以h (x)min=h (1)=4,
因为对一切x∈(0,+∞),2f(x)≥g (x)恒成立,
所以a≤h (x)min=4.……10分
(III)问题等价于证明xlnx>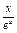 -
- (x∈(0,+∞)),
(x∈(0,+∞)),
由(I)可知f (x)=xlnx(x∈(0,+∞))的最小值是-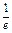 ,当且仅当x=
,当且仅当x=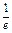 时取到.
时取到.
设m (x)=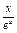 -
- (x∈(0,+∞)),则m ′(x)=
(x∈(0,+∞)),则m ′(x)=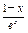 ,
,
易得m (x)max=m (1)=-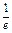 ,当且仅当x=1时取到,
,当且仅当x=1时取到,
从而对一切x∈(0,+∞),都有lnx>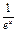 -
-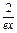 . ……14分
. ……14分
解析


科目:高中数学 来源: 题型:解答题
(本题满分12分)已知函数 .
.
(1)若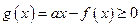 对任意
对任意 恒成立
恒成立 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若函数 的图像与直线
的图像与直线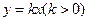 有且仅有三个公共点,且公共点的横坐标的最大值为
有且仅有三个公共点,且公共点的横坐标的最大值为 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设f(x)是定义在[-1,1]上的奇函数,且对任意的实数a,b∈[-1,1],当a+b
≠0时,都有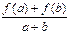 >0.
>0.
(1)若a>b,试比较f(a)与f(b)的大小;
(2)解不等式f(x -
-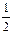 )<f(x-
)<f(x-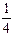 );
);
(3)如果g(x)=f(x-c)和h(x)=f(x-c2)这两个函数的定义域的交集是空集,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少时,零件的实际出厂单价恰为51元;
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少?如果订购1 000个,利润又是多少?(工厂售出一个零件的利润=实际出厂单价-成本
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com