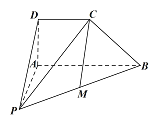
【题目】如图，在四棱锥
中, 
.
（1）若
是
的中点，求证： 
平面
；
（2）若
，求证：平面
平面
.
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）取
的中点
，利用平几知识证明四边形
是平行四边形，即得
.最后根据线面垂直判定定理得
平面
；（2）由平均知识计算
，再由
，根据线面垂直判定定理得
面
,最后根据面面垂直判定定理得平面
平面
.
试题解析：解（1）取
的中点
，连接
和
，由因为
是
的中点，
所以
是
的中位线，所以
，
由题意
，所以
，
所以四边形
是平行四边形，所以
.因为
，所以
平面
；
(2)由题意，在直角梯形
中，经计算可证得
，又
面
，
, 
面
,又
面
，所以平面
平面
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行，需转化为证明线线平行.
(2)证明线面垂直，需转化为证明线线垂直.
(3)证明线线垂直，需转化为证明线面垂直.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知函数
（
且
， 
为自然对数的底数）．
（1）若曲线
在点
处的切线斜率为0，且
有极小值，
求实数
的取值范围．
（2）当 
时，若不等式： 
在区间
内恒成立，求实数
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学为了解高一年级学生身高发育情况，对全校700名高一年级学生按性别进行分层抽样检查，测得身高（单位： 
）频数分布表如表1、表2.
表1：男生身高频数分布表
表2：女生身高频数分布表
（1）求该校高一女生的人数；
（2）估计该校学生身高在
的概率；
（3）以样本频率为概率，现从高一年级的男生和女生中分别选出1人，设
表示身高在
学生的人数，求
的分布列及数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】小华准备购买一台售价为5000元的电脑，采用分期付款方式，并在一年内将款全部付清，商场提出的 付款方式为：购买后二个月第一次付款，再过二个月第二次付款…，购买后12个月第六次付款，每次付
款金额相同，约定月利率为0.8%每月利息按复利计算．求小华每期付款的金额是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）是定义在R上的偶函数，对任意x∈R，都有f（x+4π）=f（x）+f（2π）成立，那么函数f（x）可能是（ ）
A.f（x）=2sin 
x
B.f（x）=2cos2 
x
C.f（x）=2cos2 x
D.f（x）=2cos x
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系中，O是坐标原点，两定点A，B满足| 
|=| 
|= =2，则点集{P| 
=x +y ，|x|+|y|≤1，x，y∈R}所表示的区域的面积是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是七位评委为甲，乙两名参赛歌手打出的分数的茎叶图（其中m，n为数字0～9中的一个），则甲歌手得分的众数和乙歌手得分的中位数分别为a和b，则一定有（ ）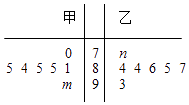 
A.a＞b
B.a＜b
C.a=b
D.a，b的大小与m，n的值有关
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=cos（ωx+ 
），（ω＞0，0＜φ＜π），其中x∈R且图象相邻两对称轴之间的距离为 
；
（1）求f（x）的对称轴方程和单调递增区间；
（2）求f（x）的最大值、最小值，并指出f（x）取得最大值、最小值时所对应的x的集合．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥P—ABCD中，平面PAD⊥底面ABCD，其中底面ABCD为等腰梯形，AD∥BC，PA＝AB＝BC＝CD＝2，PD＝2
，PA⊥PD，Q为PD的中点.
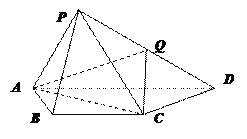
（Ⅰ）证明：CQ∥平面PAB；
（Ⅱ）求直线PD与平面AQC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com