
����Ŀ��С���ƻ���8��11����8��20���ڼ�����ij������������ξ�ͳ�����ݣ�������ڴ��ڼ䡰�������ʶȡ������������뾰�����ܲ��ź˶������˲ʱ����֮�ȣ�40%����Ϊ���ʣ�40%��60%Ϊһ�㣬60%����Ϊӵ���������ͼ��ʾ��С�����ѡ��8��11����8��19���е�ijһ�쵽��������������2��.
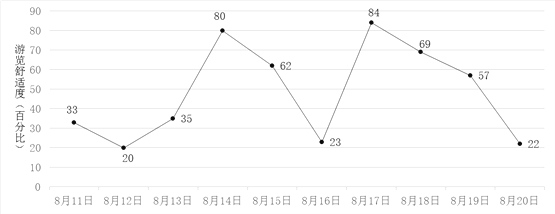 ������С���������춼����ӵ���ĸ��ʣ�
������С���������춼����ӵ���ĸ��ʣ�
������![]() ��С�������ڼ��������ʵ���������
��С�������ڼ��������ʵ���������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
������ͼ�жϴ����쿪ʼ���������������ʶȵķ���������۲�Ҫ��֤����
���𰸡���1��![]() ��2��
��2��![]() ��3����
��3����![]() ��
��![]() �տ�ʼ���������������ʶȵķ������
�տ�ʼ���������������ʶȵķ������
�����������������������![]() ��ʾ�¼���С��8��11�����
��ʾ�¼���С��8��11�����![]() ���������������������
��������������������� ![]() ����
����![]() ��ͨ���۲��ϱ���֪���춼����ӵ��Ϊ
��ͨ���۲��ϱ���֪���춼����ӵ��Ϊ![]() ���ʿɵ�����ʣ�����֪
���ʿɵ�����ʣ�����֪![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() �������
�������![]() ��
�� ![]() ��
�� ![]() ������ֲ��У�������ѧ������⼴�ɣ������ݷ�������壬��ϸ�۲�����ɵý��.
������ֲ��У�������ѧ������⼴�ɣ������ݷ�������壬��ϸ�۲�����ɵý��.
�����������![]() ��ʾ�¼���С��8��11�����
��ʾ�¼���С��8��11�����![]() ���������������������
��������������������� ![]() ��.
��.
�������⣬ ![]() ����
����![]() .
.
������![]() Ϊ�¼���С���������춼����ӵ������
Ϊ�¼���С���������춼����ӵ������
��![]() .
.
����![]() .
.
���������⣬��֪![]() �����п���ȡֵΪ
�����п���ȡֵΪ![]() ��
��
![]() ��
��
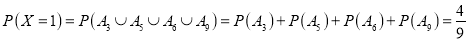 ��
��
![]() ��
��
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
|
|
|
|
|
|
|
|
��![]() ������
������![]() ��
��
����![]() ��
��![]() �տ�ʼ���������������ʶȵķ������
�տ�ʼ���������������ʶȵķ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ִ����ͼ��ʾ�ij����ͼ����������x��[��2��2]����ô�����y���ڣ� �� 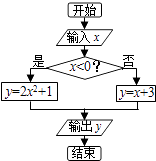
A.[5��9]
B.[3��9]
C.��1��9]
D.��3��5]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() ������
������![]() ��
�� ![]() ��
�� ![]() Ϊ��Ȼ�����ĵ���.
Ϊ��Ȼ�����ĵ���.
������![]() ��
��![]() ������
������![]() �ھ�����ͬ�ĵ����ԣ���ʵ��
�ھ�����ͬ�ĵ����ԣ���ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
������![]() ���Һ���
���Һ���![]() ����СֵΪ
����СֵΪ![]() ,��
,��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,����Բ������Ϊԭ��O,������x����,�϶���ΪA,���ҽ���ֱ�ΪF1��F2,�߶�OF1��OF2���е�ֱ�ΪB1��B2,����AB1B2�����Ϊ4��ֱ��������.
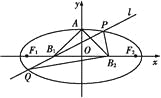
(1)�����Բ�������ʺͱ�����;
(2)��B1��ֱ�߽���Բ��P��Q����,ʹPB2��QB2,����PB2Q�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������������ij�ؾ���������������10 000�ˣ��������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ����ͼ����Ϊ�˷�����������������䡢ѧ����ְҵ�ȷ���Ĺ�ϵ��Ҫ����10 000�������÷ֲ�����������80������һ�����飬����[1 500��2 000����Ԫ���������Ӧ����� ���ˣ� 
A.15
B.16
C.17
D.18
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ά����
����![]() ����������
����������![]() ����
����![]() ��
��![]() �����
�����![]() Ϊ
Ϊ![]() ά
ά![]() ����. ��������
����. ��������![]() ά
ά![]() ����
����![]() ����
����![]() .
.
��1����![]() , ��
, ��![]() ��ֵ��
��ֵ��
��2������һ��![]() ά
ά![]() �������У�
�������� ![]() ��
��![]() �����㣺
�����㣺 ![]() ����֤���������в�����
����֤���������в�����![]() ά
ά![]() ����
����![]() .
.
(3) ����һ��![]() ά
ά![]() �������У�
�������� ![]() ��
��![]() �����㣺
�����㣺 ![]() ��������������
��������������![]() ʹ��
ʹ��![]() Ϊ
Ϊ![]() ά
ά![]() ���������е��������е�
���������е��������е�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���壺������{an}�У���a ![]() ��a
��a ![]() =p��n��2��n��N* �� pΪ���������������{an}Ϊ�ȷ������У������жϣ�
=p��n��2��n��N* �� pΪ���������������{an}Ϊ�ȷ������У������жϣ�
����{an}�ǡ��ȷ������С���������{an2}�ǵȲ����У�
��{����1��n}�ǡ��ȷ������С���
����{an}�ǡ��ȷ������С���������{akn}��k��N* �� kΪ�����������ܻ��ǡ��ȷ������С���
����{an}���ǡ��ȷ������С������ǵȲ����У���������dz����У�
������ȷ�Ľ����� �� ��д��������ȷ���۵ı�ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
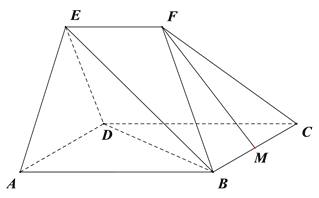
����Ŀ����ͼ���ڼ�����![]() �У�ƽ��
�У�ƽ��![]() ƽ��
ƽ��![]() ���ı���
���ı���![]() Ϊ���Σ���
������![]() ��
�� ![]() ��
�� ![]() ��
��![]() ��
�� ![]() Ϊ
Ϊ![]() �е㣮
�е㣮
������֤�� ![]() ��ƽ��
��ƽ��![]() ��
��
������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ
��ʹ![]()
![]() �� �����ڣ���
�� �����ڣ���![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�촬��˾���촬����20������֪�촬x�ҵIJ�ֵ����ΪR(x)��3 700x��45x2��10x3(��λ����Ԫ)���ɱ�����ΪC(x)��460x��5 000(��λ����Ԫ)��
(1)��������P(x)��(��ʾ������ֵ���ɱ�)
(2)�����촬�����Ŷ�����ʱ����ʹ��˾�촬�����������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com