
【题目】甲、乙两人投篮命中的概率为别为 ![]() 与
与 ![]() ,各自相互独立,现两人做投篮游戏,共比赛3局,每局每人各投一球.
,各自相互独立,现两人做投篮游戏,共比赛3局,每局每人各投一球.
(1)求比赛结束后甲的进球数比乙的进球数多1个的概率;
(2)设ξ表示比赛结束后,甲、乙两人进球数的差的绝对值,求ξ的概率分布和数学期望E(ξ).
【答案】
(1)解:比赛结束后甲的进球数比乙的进球数多1个,有以下几种情况:
甲进1球,乙进0球;甲进2球,乙进1球;甲进3球,乙进2球.
比赛结束后甲的进球数比乙的进球数多1个的概率:
p= ![]() +
+ ![]() +
+ ![]() =
= ![]()
(2)解:由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)= ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
P(ξ=2)=1﹣P(ξ=0)﹣P(ξ=1)﹣P(ξ=3)=1﹣ ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =1
=1
【解析】(1)比赛结束后甲的进球数比乙的进球数多1个,有以下几种情况:甲进1球,乙进0球;甲进2球,乙进1球;甲进3球,乙进2球.由此能求出比赛结束后甲的进球数比乙的进球数多1个的概率.(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
【考点精析】认真审题,首先需要了解随机事件(在条件S下可能发生也可能不发生的事件,叫相对于条件S的随机事件),还要掌握离散型随机变量及其分布列(在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
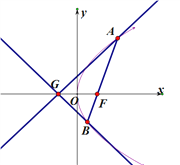
(1)求抛物线![]() 的方程;
的方程;
(2)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的单调区间及极值;
(2)求证:当a>ln2﹣1且x>0时,ex>x2﹣2ax+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某港湾的平面示意图如图所示, ![]() ,
, ![]() ,
, ![]() 分别是海岸线
分别是海岸线![]() 上的三个集镇,
上的三个集镇, ![]() 位于
位于![]() 的正南方向6km处,
的正南方向6km处, ![]() 位于
位于![]() 的北偏东
的北偏东![]() 方向10km处.
方向10km处.
(Ⅰ)求集镇![]() ,
, ![]() 间的距离;
间的距离;
(Ⅱ)随着经济的发展,为缓解集镇![]() 的交通压力,拟在海岸线
的交通压力,拟在海岸线![]() 上分别修建码头
上分别修建码头![]() ,开辟水上航线.勘测时发现:以
,开辟水上航线.勘测时发现:以![]() 为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头
为圆心,3km为半径的扇形区域为浅水区,不适宜船只航行.请确定码头![]() 的位置,使得
的位置,使得![]() 之间的直线航线最短.
之间的直线航线最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知长方体ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 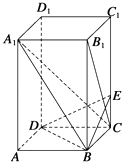
(1)求CE的长;
(2)求证:A1C⊥平面BED;
(3)求A1B与平面BDE夹角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若奇函数f(x)在其定义域R上是减函数,且对任意的x∈R,不等式f(cos2x+sinx)+f(sinx﹣a)≤0恒成立,则a的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com