分析:先以D为原点建立空间直角坐标系,写出相关点的坐标,(1)先利用线面垂直的判定定理求平面ABC
1D
1的法向量,再求
与此法向量的夹角的余弦值,其绝对值就是线面角的正弦值;
(2)设
=λ
,将
用λ表示,要使MN∥A
1C,只需存在μ,使
=μ
,列方程组即可解得λ的值,从而确定N点位置
解答:解:如图建立空间直角坐标系:设正方体棱长为1
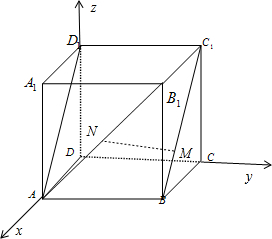
则D(0,0,0),A(1,0,0),B(1,1,0),C
1(0,1,1),D
1(0,0,1),B
1(1,1,1),A
1(1,0,1),C(0,1,0)
(1)
=(0,1,1),
=(-1,0,1),
=(0,1,0)
设平面ABC
1D
1所的法向量为
=(x,y,z)
则
.取
=(1,0,1)
cos<
,
>=
=
=
设直线AB
1和平面ABC
1D
1所成的角为θ
则sinθ=
,又θ∈[0,
]
∴θ=
∴直线AB
1和平面ABC
1D
1所成的角为
(2)
=(-1,1,-1),
=(-1,0,1),
∵BM=
BC1,
∴
=
=(-
,0,
)
设
=λ
=λ(0,-1,-1)=(0,-λ,-λ)
则
=
+
+
=(
,0,-
)+(0,0,1)+(0,-λ,-λ)=(
,-λ,
-λ)
∵MN∥A
1C.
∴(
,-λ,
-λ)=μ(-1,1,-1),∴
解得λ=
∴当
=
时,MN∥A
1C.
点评:本题主要考查了空间线面角的求法,空间线线平行的判定,空间直角坐标系与空间向量在解题中的应用,需要有较强的运算能力

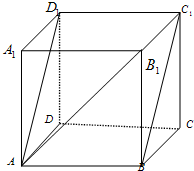 正方体ABCD-A1B1C1D1中,
正方体ABCD-A1B1C1D1中, 则D(0,0,0),A(1,0,0),B(1,1,0),C1(0,1,1),D1(0,0,1),B1(1,1,1),A1(1,0,1),C(0,1,0)
则D(0,0,0),A(1,0,0),B(1,1,0),C1(0,1,1),D1(0,0,1),B1(1,1,1),A1(1,0,1),C(0,1,0)

 阅读快车系列答案
阅读快车系列答案 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.