
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
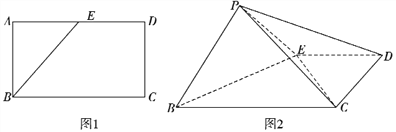
为线段![]() 的中点,如图1,沿
的中点,如图1,沿![]() 将
将![]() 折起至
折起至![]() ,使
,使![]() ,如图2所示.
,如图2所示.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由已知条件证明出![]() 平面
平面![]() ,根据面面垂直的判定定理证明出平面
,根据面面垂直的判定定理证明出平面![]() 平面
平面![]() ;(2)取BE的中点为
;(2)取BE的中点为![]() ,以
,以![]() 为坐标原点,以过点
为坐标原点,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,过点
轴,过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,建立空间直角坐标系,写出各点坐标,设平面
轴,建立空间直角坐标系,写出各点坐标,设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,由线面垂直的性质定理,分别求出
,由线面垂直的性质定理,分别求出![]() 的坐标,求出二面角的余弦值。
的坐标,求出二面角的余弦值。
试题解析:
(1)证明:在图1中连接![]() ,则
,则![]()
![]() ,
,![]() ,
,![]() .
.
∵![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]()
![]() 平面
平面![]() .
.
(2)解:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
以![]() 为坐标原点,以过点
为坐标原点,以过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,过点
轴,过点![]() 且平行于
且平行于![]() 的直线为
的直线为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,建立如图所示的直角坐标系,则
轴,建立如图所示的直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
由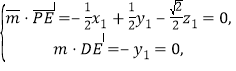 可得
可得![]() ;
;
由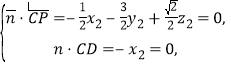 可得
可得![]() ;
;
则![]() ,由图形知二面角
,由图形知二面角![]() 的平面角为钝二面角,
的平面角为钝二面角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x) .
.

(1)画出函数f(x)的图象,根据图象直接写出f(x)的值域;
(2)根据图象直接写出满足f(x)≥2的所有x的集合;
(3)若f(x)的递减区间为(﹣∞,a),递增区间为(b,+∞),直接写出a的最大值,b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
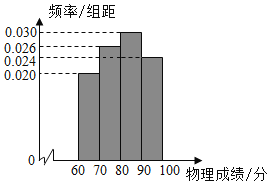
【题目】为了解某校高一1000名学生的物理成绩,随机抽查了部分学生的期中考试成绩,将数据整理后绘制成如图所示的频率分布直方图.
(1)估计该校高一学生物理成绩不低于80分的人数;
(2)若在本次考试中,规定物理成绩在m分以上(包括m分)的为优秀,该校学生物理成绩的优秀率大约为18%,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人组成一个小组参加电视台举办的听曲猜歌名活动,在每一轮活动中,依次播放三首乐曲,然后甲猜第一首,乙猜第二首,丙猜第三首,若有一人猜错,则活动立即结束;若三人均猜对,则该小组进入下一轮,该小组最多参加三轮活动.已知每一轮甲猜对歌名的概率是![]() ,乙猜对歌名的概率是
,乙猜对歌名的概率是![]() ,丙猜对歌名的概率是
,丙猜对歌名的概率是![]() ,甲、乙、丙猜对与否互不影响.
,甲、乙、丙猜对与否互不影响.
(I)求该小组未能进入第二轮的概率;
(Ⅱ)记乙猜歌曲的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 直线AM,BM相交于点M,且它们的斜率之和为2.
直线AM,BM相交于点M,且它们的斜率之和为2.
(1)设![]() 且
且![]() ,求
,求![]() 的表达式,并写出函数
的表达式,并写出函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性?并给出证明;
的奇偶性?并给出证明;
(3)试用函数单调性的定义证明:![]() 在定义域上不是增函数,但在(0,1)∪(1,+
在定义域上不是增函数,但在(0,1)∪(1,+![]() )上为增函数.
)上为增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com