
【题目】执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5
B.4
C.3
D.2
【答案】D
【解析】解:由题可知初始值t=1,M=100,S=0,
要使输出S的值小于91,应满足“t≤N”,
则进入循环体,从而S=100,M=﹣10,t=2,
要使输出S的值小于91,应接着满足“t≤N”,
则进入循环体,从而S=90,M=1,t=3,
若此时输出S,则S的值小于91,故t=3应不满足“t≤N”,跳出循环体,
所以输入的N的最小值为2,
故选:D.
【考点精析】利用算法的循环结构和程序框图对题目进行判断即可得到答案,需要熟知在一些算法中,经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构,循环结构可细分为两类:当型循环结构和直到型循环结构;程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


科目:高中数学 来源: 题型:
【题目】在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图(1)将△AEF沿EF折起到△A1EF的位置,使二面角A1﹣EF﹣B成直二面角,连结A1B、A1P(如图(2)). 
(1)求证:A1E⊥平面BEP;
(2)求二面角B﹣A1P﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐的单音色旋律,选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.

(Ⅰ) 完成下列2×2列联表;
正误 年龄 | 正确 | 错误 | 合计 |
20~30 | 30 | ||
30~40 | 70 | ||
合计 | 120 |
(Ⅱ)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为( )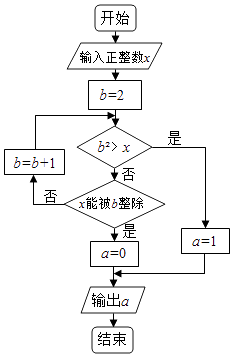
A.0,0
B.1,1
C.0,1
D.1,0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=ex+2x2-3x.
(1)求证:函数f (x)在区间[0,1]上存在唯一的极值点.
(2)当x≥![]() 时,若关于x的不等式f (x)≥
时,若关于x的不等式f (x)≥![]() x2+(a-3)x+1恒成立,试求实数a的取值范围.
x2+(a-3)x+1恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcosθ=4.
(Ⅰ)M为曲线C1上的动点,点P在线段OM上,且满足|OM||OP|=16,求点P的轨迹C2的直角坐标方程;
(Ⅱ)设点A的极坐标为(2, ![]() ),点B在曲线C2上,求△OAB面积的最大值.
),点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 是满足下列条件的函数
是满足下列条件的函数![]() 的全体:在定义域内存在实数
的全体:在定义域内存在实数![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)判断幂函数![]() 是否属于集合
是否属于集合![]() ?并说明理由;
?并说明理由;
(Ⅱ)设![]() ,
, ![]() ,
,
i)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
ii)若对任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)为考察某种药物预防疾病的效果,进行动物试验,调查了105个样本,统计结果为:服药的共有55个样本,服药但患病的仍有10个样本,没有服药且未患病的有30个样本.
(1)根据所给样本数据完成2×2列联表中的数据;
(2)请问能有多大把握认为药物有效?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对一个样本容量为100的数据分组,各组的频数如表:
区间 | [17,19) | [19,21) | [21,23) | [23,25) | [25,27) | [27,29) | [29,31) | [31,33] |
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的( )
A. 16% B. 40% C. 42% D. 58%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com