
【题目】已知函数![]() ,
, ![]() .
.
(1)试比较![]() 与
与![]() 的大小关系,并给出证明;
的大小关系,并给出证明;
(2)解方程: ![]() ;
;
(3)求函数![]() ,
, ![]() (
(![]() 是实数)的最小值.
是实数)的最小值.
【答案】(1)![]() (2)
(2)![]() 或
或![]() .(3)
.(3)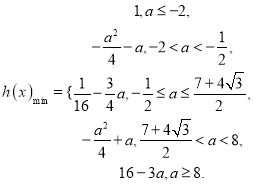
【解析】试题分析:(1)![]() 与
与![]() 作差,配方后即可得
作差,配方后即可得![]() ;(2)原方程化为
;(2)原方程化为![]() ,设
,设![]() ,可得
,可得![]() ,进而可得结果;(3)令
,进而可得结果;(3)令![]() ,则
,则![]() ,函数
,函数![]() 可化为
可化为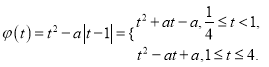 ,利用二次函数的性质分情况讨论,分别求出两段函数的最小值,比较大小后可得各种情况下函数
,利用二次函数的性质分情况讨论,分别求出两段函数的最小值,比较大小后可得各种情况下函数![]() ,
, ![]() (
(![]() 是实数)的最小值.
是实数)的最小值.
试题解析:(1)因为![]() ,
,
所以![]() .
.
(2)由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() ,故原方程可化为
,故原方程可化为![]() ,
,
解得![]() ,或
,或![]() (舍去),
(舍去),
则![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() 或
或![]() .
.
(3)令![]() ,则
,则![]() ,
,
函数![]() 可化为
可化为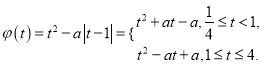
①若![]() ,
,
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ,
,
故![]() ,
, ![]() .
.
②若![]() ,
,
当![]() ,
, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ,
,
故![]() ,
, ![]() .
.
③若![]() ,
,
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ,故
,故![]() ,
, ![]() ;
;
④若![]() ,
,
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ,
,
则![]() 时,
时, ![]() ,
,
![]() 时,
时, ![]() ,
,
故![]() ,
, 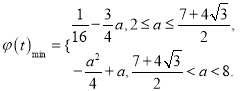
⑤若![]() ,
,
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ;
;
当![]() 时,
时, ![]() ,对称轴
,对称轴![]() ,此时
,此时![]() ,
,
因为![]() 时,
时, ![]() ,
,
故![]() ,
, ![]() .
.
综述: 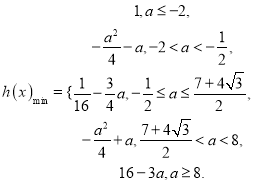


科目:高中数学 来源: 题型:
【题目】如图所示,抛物线C:y2=2px(p>0)的焦点为F,经过点F的直线l与抛物线交于P,Q两点,弦PQ的中点为N,经过点N作y轴的垂线与C的准线交于点T.
(Ⅰ)若直线l的斜率为1,且|PQ|=4,求抛物线C的标准方程;
(Ⅱ)证明:无论p为何值,以线段TN为直径的圆总经过点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)设函数![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(2)定义![]() 表示
表示![]() 中较小者,设函数
中较小者,设函数![]()
![]() .
.
①求函数![]() 的单调区间及最值;
的单调区间及最值;
②若关于![]() 的方程
的方程![]() 有两个不同的实根,求实数
有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 ![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C:ρ=2
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C:ρ=2 ![]() cos(θ﹣
cos(θ﹣ ![]() ).
).
(Ⅰ) 求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ) 求曲线C上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了研究年宣传费![]() (单位:千元)对销售量
(单位:千元)对销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:千元)的影响,搜集了近 8 年的年宣传费
(单位:千元)的影响,搜集了近 8 年的年宣传费![]() 和年销售量
和年销售量![]() 数据:
数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 38 | 40 | 44 | 46 | 48 | 50 | 52 | 56 |
| 45 | 55 | 61 | 63 | 65 | 66 | 67 | 68 |
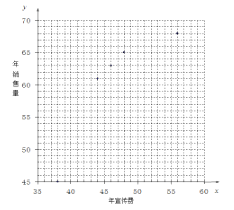
(Ⅰ)请补齐表格中 8 组数据的散点图,并判断![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的函数表达式?(给出判断即可,不必说明理由)
的函数表达式?(给出判断即可,不必说明理由)
(Ⅱ)若(Ⅰ)中的![]() ,且产品的年利润
,且产品的年利润![]() 与
与![]() ,
, ![]() 的关系为
的关系为![]() ,为使年利润值最大,投入的年宣传费 x 应为何值?
,为使年利润值最大,投入的年宣传费 x 应为何值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为 ![]() ,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
ξ | 0 | 1 | 2 | 3 |
p |
| x | y |
|
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com