练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】（题文）（2017·长春市二模）如图，在四棱锥中，底面是菱形，，平面，，点，分别为和中点.

    （1）求证：直线平面；

    （2）求与平面所成角的正弦值.

    【答案】(1)见解析.

    (2) .

    【解析】

    试题分析：（1）作交于根据条件可证得为平行四边形，从而根据线面平行的判定，即可得证；（2）建立空间直角坐标系，根据条件中的数据可求得平面平面PAB的一个法向量为，从而问题可等价转化为求与的夹角．

    试题解析：（1）作交于，∵点为中点，∴，∴，∴为平行四边形，∴，∵平面，平面，∴平面；（2）∵，∴，如图所示，建立坐标系，则，，，

    ，，∴，，设平面的一个法向量为，∵，，∴，取，则，∴平面PAB的一个法向量为，∵，∴设向量与所成角为，

    ∴，∴平面所成角的正弦值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】经济订货批量模型，是目前大多数工厂、企业等最常采用的订货方式，即某种物资在单位时间的需求量为某常数，经过某段时间后，存储量消耗下降到零，此时开始订货并随即到货，然后开始下一个存储周期，该模型适用于整批间隔进货、不允许缺货的存储问题，具体如下：年存储成本费（元）关于每次订货（单位）的函数关系，其中为年需求量，为每单位物资的年存储费，为每次订货费. 某化工厂需用甲醇作为原料，年需求量为6000吨，每吨存储费为120元/年，每次订货费为2500元.

    （1）若该化工厂每次订购300吨甲醇，求年存储成本费；

    （2）每次需订购多少吨甲醇，可使该化工厂年存储成本费最少？最少费用为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“90后”指1990年及以后出生，“80后”指1980-1989年之间出生，“80前”指1979年及以前出生.某调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业岗位分布条形图，则下列结论中不一定正确的是（ ）

    A.互联网行业从业人员中90后占一半以上

    B.互联网行业中从事技术岗位的人数超过总人数的

    C.互联网行业中从事运营岗位的人数90后比80前多

    D.互联网行业中从事技术岗位的人数90后比80后多

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若在区间内单调递增，求的取值范围；

    （2）若在区间内存在极大值，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”．类似的，我们在平面向量集上也可以定义一个称“序”的关系，记为“”．定义如下：对于任意两个向量，“”当且仅当“”或“”。按上述定义的关系“”，给出如下四个命题：

    ①若，则；

    ②若，则；

    ③若，则对于任意；

    ④对于任意向量，若，则。

    其中真命题的序号为__________

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若正项数列满足：，则称此数列为“比差等数列”．

    （1）试写出一个“比差等数列”的前项；

    （2）设数列是一个“比差等数列”，问是否存在最小值，如存在，求出最小值；如不存在，请说明理由；

    （3）已知数列是一个“比差等数列”，为其前项的和，试证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本题满分12分） 如图，的外接圆的半径为，所在的平面，，，，且，．

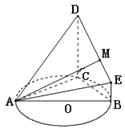
    （1）求证：平面ADC平面BCDE．

    （2）试问线段DE上是否存在点M，使得直线AM与平面ACD所成角的正弦值为？若存在，

    确定点M的位置，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知实数，函数.

    （1）当时，求函数的值域；

    （2）当时，判断函数的单调性，并证明；

    （3）求实教的范围，使得对于区间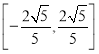上的任意三个实数，都存在以为边长的三角形.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数是定义在上的奇函数，且为偶函数，当时，，若有三个零点，则实数的取值集合是________.

    查看答案和解析>>

    同步练习册答案