
 ?
?
 •
•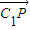 =0即可得到结论;
=0即可得到结论;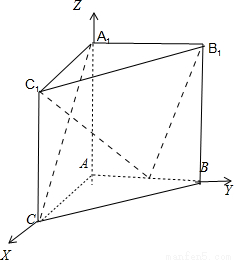
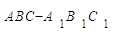 =
= AB×AC×AA1=1,∴AB=2.(2分)
AB×AC×AA1=1,∴AB=2.(2分)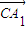 =(-1,0,1),
=(-1,0,1),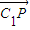 =(-1,m,-1),
=(-1,m,-1),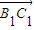 =(-1,2,0)
=(-1,2,0)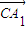 •
•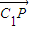 =(-1)×(-1)+0×m+1×(-1)=0,
=(-1)×(-1)+0×m+1×(-1)=0,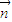 =(x,y,z),
=(x,y,z),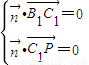 ⇒
⇒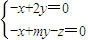
 =(2,1,m-2),(9分)
=(2,1,m-2),(9分)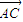 =(1,0,0),
=(1,0,0),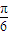 =
=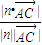 =
=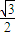 ,
,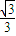 (舍去)或m=2-
(舍去)或m=2- .
.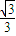 时,二面角C1-PB1-A1的大小为
时,二面角C1-PB1-A1的大小为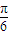 .(12分)
.(12分)

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
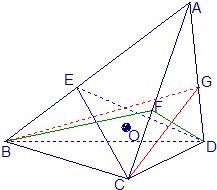 如图,在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G,使AE:EB=AF:FC=AG:GD=2:1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O-BCD的体积等于( )
如图,在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G,使AE:EB=AF:FC=AG:GD=2:1,记O为三平面BCG、CDE、DBF的交点,则三棱锥O-BCD的体积等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
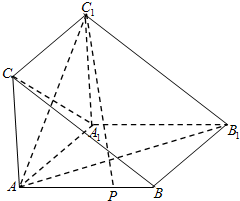 如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC⊥AB,AC=AA1=1,P为线段AB上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
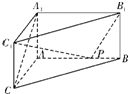 (2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.
(2012•蓝山县模拟)如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.| π | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B
B![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com