
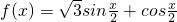
 sin
sin +
+ cos
cos )=2sin(
)=2sin( +
+ )
)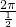 =4π
=4π +
+ =kπ,得x=2kπ-
=kπ,得x=2kπ-
 ,0)
,0) +
+ =kπ+
=kπ+ ,得x=2kπ+
,得x=2kπ+

 ≤
≤ +
+ ≤2kπ+
≤2kπ+
 ≤x≤4kπ+
≤x≤4kπ+
 ,4kπ+
,4kπ+ ]
] ,
,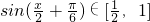
 +
+ ),然后根据T=
),然后根据T=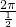 =4π,对称中心
=4π,对称中心 +
+ =kπ,对称轴
=kπ,对称轴 +
+ =kπ+
=kπ+ ,单调递增区间2kπ-
,单调递增区间2kπ- ≤
≤ +
+ ≤2kπ+
≤2kπ+ ,再将x求出即可.
,再将x求出即可. ,然后根据正弦函数的特点求出值域.
,然后根据正弦函数的特点求出值域.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:《第2章 基本初等函数(Ⅰ)》2012年单元测试卷(南宁外国语学校)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省宿州市泗县双语中学高一(上)期中数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011-2012学年天津一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
 .
. 上的最大值和最小值.
上的最大值和最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省保定二中高三第三次大考数学试卷(文理合卷)(解析版) 题型:解答题
 .
. 上的最大值和最小值.
上的最大值和最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com