
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1= .
.

(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
(1)见解析(2)θ=
【解析】(1)由题设易知OA,OB,OA1两两垂直,以O为原点建立直角坐标系,如图.

∵AB=AA1= ,
,
∴OA=OB=OA1=1,
∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),
A1(0,0,1).由 =
= ,易得B1(-1,1,1).
,易得B1(-1,1,1).
∵ =(-1,0,-1),
=(-1,0,-1), =(0,-2,0),
=(0,-2,0), =(-1,0,1).
=(-1,0,1).
∴ ·
· =0,
=0, ·
· =0,
=0,
∴A1C⊥BD,A1C⊥BB1,
又BD∩BB1=B,
∴A1C⊥平面BB1D1D.
(2)设平面OCB1的法向量n=(x,y,z).
∵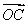 =(-1,0,0),
=(-1,0,0), =(-1,1,1),
=(-1,1,1),
∴ ∴
∴ 取n=(0,1,-1),
取n=(0,1,-1),
由(1)知, =(-1,0,-1)是平面BB1D1D的法向量,
=(-1,0,-1)是平面BB1D1D的法向量,
∴cos θ=|cos〈n, 〉|=
〉|= =
= .
.
又∵0≤θ≤ ,∴θ=
,∴θ=


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用2练习卷(解析版) 题型:填空题
已知函数f(x)=-x2-2x,g(x)=
(1)g[f(1)]=________;
(2)若方程g[f(x)]-a=0的实数根的个数有4个,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用1练习卷(解析版) 题型:填空题
已知函数f(x)=x3+x,对任意的m∈[-2,2],f(mx-2)+f(x)<0恒成立,则x的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用18练习卷(解析版) 题型:解答题
已知 的展开式的二项式系数之和比(a+b)2n的展开式的系数之和小240,求
的展开式的二项式系数之和比(a+b)2n的展开式的系数之和小240,求 n的展开式中系数最大的项.
n的展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用17练习卷(解析版) 题型:解答题
无锡学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设ξ为选出的人中既会唱歌又会跳舞的人数,且P(ξ>0)=
(1)求文娱队的队员人数;
(2)写出ξ的概率分布列并计算E(ξ).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用15练习卷(解析版) 题型:解答题
在极坐标系中,已知圆ρ=2cos θ与直线3ρcos θ+4ρsin θ+a=0相切,求实数a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用14练习卷(解析版) 题型:解答题
设函数f(x)=|2x+1|-|x-4|.
(1)解不等式f(x)>2;
(2)求函数y=f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(解析版) 题型:填空题
已知双曲线C与椭圆 =1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于________.
=1有共同的焦点F1,F2,且离心率互为倒数.若双曲线右支上一点P到右焦点F2的距离为4,则PF2的中点M到坐标原点O的距离等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练4练习卷(解析版) 题型:选择题
已知函数y=Asin(ωx+φ)+m的最大值为4,最小值为0.两个对称轴间最短距离为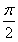 ,直线x=
,直线x= 是其图象的一条对称轴,则符合条件的解析式为( )
是其图象的一条对称轴,则符合条件的解析式为( )
A.y=4sin  B.y=-2sin
B.y=-2sin  +2
+2
C.y=-2sin  D.y=2sin
D.y=2sin  +2
+2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com