
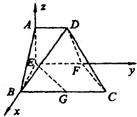
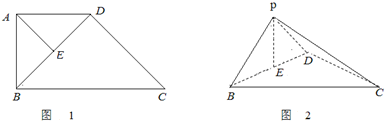
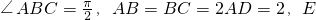 、F分别为线段AB、CD的动点,且EF∥BC,G是BC的中点,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图2).
、F分别为线段AB、CD的动点,且EF∥BC,G是BC的中点,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图2).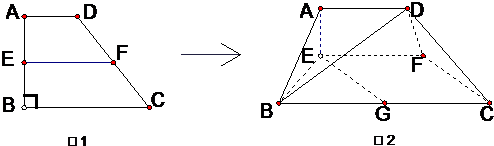
 =(t-2,1,t),
=(t-2,1,t),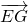 =(2-t,1,0).
=(2-t,1,0).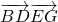 =0,即-(t-2)2+1=0,解得 t=1 或t=3(舍去).
=0,即-(t-2)2+1=0,解得 t=1 或t=3(舍去). ,0 ),D(0,1,1 ),
,0 ),D(0,1,1 ), =(-1,1,1),
=(-1,1,1), =(-1,0 1),
=(-1,0 1), =(-1,
=(-1, ,0 ).
,0 ). =(a,b,1),由
=(a,b,1),由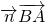 =0,
=0,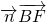 =0,解得 a=-1,b=1,故
=0,解得 a=-1,b=1,故  =(-1,1,1).
=(-1,1,1). ,
, >=
>=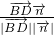 =
=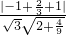 =
=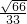 ,
,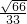 .
. 
 和
和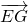 的坐标,由BD⊥EG,得
的坐标,由BD⊥EG,得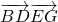 =0,解方程求得t的值.
=0,解方程求得t的值. 、
、 的坐标,设出平面ABF的法向量为
的坐标,设出平面ABF的法向量为 的坐标,由
的坐标,由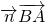 =0,
=0,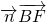 =0,解得
=0,解得 的坐标,设BD与平面ABF所成角为θ,则由sinθ=cos<
的坐标,设BD与平面ABF所成角为θ,则由sinθ=cos< ,
, >
>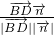 ,运算求得结果,即可得到θ的值.
,运算求得结果,即可得到θ的值.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:肇庆二模 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
已知如图四棱锥P—ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(I)求异面直线PA与CD所成的角的大小;
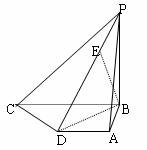 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;
(III)求二面角A—PD—B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
已知如图四棱锥P—ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(I)求异面直线PA与CD所成的角的大小;
 (II)求证:BE⊥平面PCD;
(II)求证:BE⊥平面PCD;
(III)求二面角A—PD—B的大小.
查看答案和解析>>
科目:高中数学 来源:《立体几何》2013年广东省十二大市高三二模数学试卷汇编(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com