
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,设函数
,设函数![]() 在
在![]() 上的极值点为
上的极值点为![]() ,求证:
,求证: ![]() .
.
【答案】(1)当![]() 时,
时, ![]() 的极大值为
的极大值为![]() ,无极小值;(2)
,无极小值;(2) ![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)求导,利用导函数的符号变化得到函数的单调性,进而得到函数的极值;(2)求导,将函数在某区间上单调递增转化为导函数非负恒成立,分离参数,构造函数,将不等式恒成立问题转化为求函数的最值问题;(3)连续两次求导,分别通过研究导函数的符号变化研究函数的极值,再作差构造函数,将不等式恒成立问题转化为求函数的最值问题,再利用求导进行求解.
试题解析:(1)当![]() 时,
时, ![]() ,定义域为
,定义域为![]() ,
,
![]() ,令
,令![]() ,得
,得![]() .
.
|
|
|
|
|
|
|
|
|
| 极大值 |
|
![]() 当
当![]() 时,
时, ![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(2)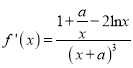 ,由题意
,由题意![]() 对
对![]() 恒成立.
恒成立.
![]()
![]() ,
, ![]() ,
,
![]()
![]() 对
对![]() 恒成立,
恒成立,
![]()
![]() 对
对![]() 恒成立.
恒成立.
令![]() ,
, ![]() ,则
,则![]() ,
,
①若![]() ,即
,即![]() ,则
,则![]() 对
对![]() 恒成立,
恒成立,
![]()
![]() 在
在![]() 上单调递减,
上单调递减,
则![]() ,
, ![]() ,
, ![]() 与
与![]() 矛盾,舍去;
矛盾,舍去;
②若![]() ,即
,即![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
![]() 当
当![]() 时,
时, 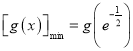
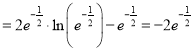 ,
,
![]() .综上
.综上![]() .
.
(3)当![]() 时,
时, ![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
则![]()
![]() ,令
,令![]() ,得
,得![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减, 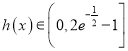 ,
,
![]() 恒成立,
恒成立, ![]() 单调递减,且
单调递减,且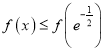 .
.
②当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
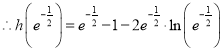
![]()
又![]()
![]() ,
,
![]() 存在唯一
存在唯一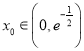 ,使得
,使得![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
当![]() 时,
时, ![]() ,
, ![]() 单调递减,且
单调递减,且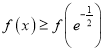 ,
,
由①和②可知, ![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,
上单调递减,
![]() 当
当![]() 时,
时, ![]() 取极大值.
取极大值.
![]() ,
, ![]() ,
,
![]()
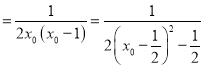 ,
,
又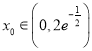 ,
, ![]() ,
, 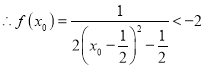 .
.


科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式e2x﹣alnx![]() a恒成立,则实数a的取值范围是( )
a恒成立,则实数a的取值范围是( )
A.[0,2e]B.(﹣∞,2e]C.[0,2e2]D.(﹣∞,2e2]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(
两点(![]() 两点相邻).
两点相邻).
(Ⅰ)若![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)过![]() 两点分别作曲线
两点分别作曲线![]() 的切线
的切线![]() ,两切线交于点
,两切线交于点![]() ,求
,求![]() 与
与![]() 面积之积的最小值.
面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形![]() 挖去扇形
挖去扇形![]() 后构成的).已知
后构成的).已知![]() ,线段
,线段![]() 与弧
与弧![]() 、弧
、弧![]() 的长度之和为
的长度之和为![]() 米,圆心角为
米,圆心角为![]() 弧度.
弧度.

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)记铭牌的截面面积为![]() ,试问
,试问![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某船在海面![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向,与
方向,与![]() 相距
相距![]() 海里,测得灯塔
海里,测得灯塔![]() 在北偏西
在北偏西![]() 方向,与
方向,与![]() 相距
相距![]() 海里,船由
海里,船由![]() 向正北方向航行到
向正北方向航行到![]() 处,测得灯塔
处,测得灯塔![]() 在南偏西
在南偏西![]() 方向,这时灯塔
方向,这时灯塔![]() 与
与![]() 相距多少海里?
相距多少海里?![]() 在
在![]() 的什么方向?
的什么方向?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com