
【题目】直线![]() 与抛物线
与抛物线![]()
![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,若
,若![]() ,
,![]() 到
到![]() 轴距离的乘积为
轴距离的乘积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设点![]() 为抛物线
为抛物线![]() 的焦点,当
的焦点,当![]() 面积最小时,求直线
面积最小时,求直线![]() 的方程.
的方程.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点F到左顶点的距离为3.
的右焦点F到左顶点的距离为3.
(1)求椭圆C的方程;
(2)设O是坐标原点,过点F的直线与椭圆C交于A,B两点(A,B不在x轴上),若![]() ,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
,延长AO交椭圆与点G,求四边形AGBE的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
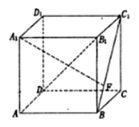
A.无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
B.当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
C.无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
D.当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月1日,是中华人民共和国成立70周年纪念日.70年砥砺奋进,70年波澜壮阔,感染、激励着一代又一代华夏儿女,为祖国的繁荣昌盛努力拼搏,奋发图强.为进一步对学生进行爱国教育,某校社会实践活动小组,在老师的指导下,从学校随机抽取四个班级160名同学对这次国庆阅兵受到激励情况进行调查研究,记录的情况如下图:

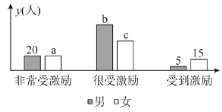
(1)如果从这160人中随机选取1人,此人非常受激励的概率和此人是很受激励的女同学的概率都是![]() ,求
,求![]() 的值;
的值;
(2)根据“非常受激励”与“很受激励”两种情况进行研究,判断是否有![]() 的把握认为受激励程度与性别有关.
的把握认为受激励程度与性别有关.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
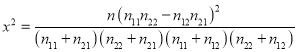
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 处有极值,且
处有极值,且![]() ,则称
,则称![]() 为函数
为函数![]() 的“F点”.
的“F点”.
(1)设函数![]() (
(![]() ).
).
①当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
②若函数![]() 存在“F点”,求k的值;
存在“F点”,求k的值;
(2)已知函数![]() (a,b,
(a,b,![]() ,
,![]() )存在两个不相等的“F点”
)存在两个不相等的“F点”![]() ,
,![]() ,且
,且![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥P-ABC中,平面PAB⊥平面ABC,△ABC是边长为![]() 的等边三角形,
的等边三角形,![]() ,点O,M分别是AB,BC的中点.
,点O,M分别是AB,BC的中点.
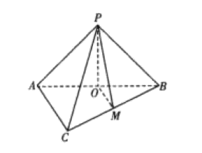
(1)证明:AC//平面POM;
(2)求点B到平面POM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
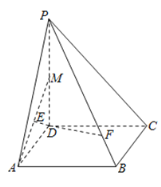
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 底面ABCD,且
底面ABCD,且![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com