
【题目】已知![]() .
.
(1)证明![]() 在
在![]() 上为增函数;
上为增函数;
(2)当![]() 时,解不等式
时,解不等式![]() ;
;
(3)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大整数值.
的最大整数值.
【答案】(1)见解析(2)![]() (3)0
(3)0
【解析】试题分析:
(1)首先求得函数的导函数,然后对![]() 进行二次求导可得
进行二次求导可得![]() 在
在![]() 上为增函数;
上为增函数;
(2)利用(1)中函数的单调性结合题意可得不等式的解集为![]()
(3)不等式即![]() ,构造新函数
,构造新函数![]() ,结合导函数的性质可得
,结合导函数的性质可得![]() 的最大整数值为0.
的最大整数值为0.
试题解析:
解:(1)![]() ,设
,设![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
|
|
|
|
| - | 0 | + |
| ↓ | 极小值 | ↑ |
![]()
![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() 在
在![]() 上为增函数.
上为增函数.
(2)![]() 时,
时, ![]() ,
, ![]()
![]() 在
在![]() 上为增函数,
上为增函数,
![]() 若
若![]() ,则
,则![]() ,与
,与![]() 矛盾;
矛盾;
若![]() ,则
,则![]() ,
, ![]() 成立.
成立.
经化简![]() ,则
,则![]() ,
, ![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]() 设
设![]() ,
,
![]()
![]() ,
,
![]()
![]() 在
在![]() 上为增函数,
上为增函数, ![]()
![]() ,得
,得![]() ,
,
![]() 原不等式解集为
原不等式解集为![]() .
.
(3)![]()
![]() 在
在![]() 上为增函数,
上为增函数, ![]()
![]() ,即
,即![]() ,令
,令
![]() ,
, ![]()
![]() ,
,
设![]() ,
, ![]() ,
,
![]()
![]() 时,
时, ![]() ,
, ![]() ,
,
![]()
![]() 在
在![]() 为增函数,
为增函数,
![]()
![]() 在
在![]() 为增函数,
为增函数,
![]() ,
, 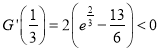 ,
,
![]()
![]() 有任一解,设为
有任一解,设为![]() ,
,
![]()
![]() 时,
时,
|
|
|
|
| - | 0 | + |
| ↓ | 极 | ↑ |
![]()
![]()
![]() ,
,
![]()
![]() 即
即![]() ,
,
![]()
![]()
![]() ,
,
又![]()
![]() ,
, ![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 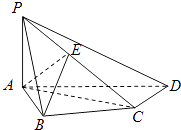
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,则实数a的取值范围是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线c1:y2=2px(p>0)与曲线c2:(x﹣6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且 ![]() =0.
=0. 
(1)求曲线c1的方程;
(2)过定点M(3,2)的直线l与曲线c1交于A,B两点,若点M是线段AB的中点,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O、E分别是BD、BC的中点,CA=CB=CD=BD=2,AB=AD= ![]() .
.
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦;
(Ⅲ)求点E到平面ACD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足an+1>an , a1=1,且该数列的前三项分别加上1,1,3后顺次成为等比数列{bn}的前三项.
(1)求数列{an},{bn}的通项公式;
(2)令cn=anbn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一学生周末的“阅读时间”,从高一年级中随机抽取了![]() 名学生进行调査,获得了每人的周末“阅读时间”(单位:小时),按照
名学生进行调査,获得了每人的周末“阅读时间”(单位:小时),按照![]() 分成
分成![]() 组,制成样本的频率分布直方图如图所示:
组,制成样本的频率分布直方图如图所示:
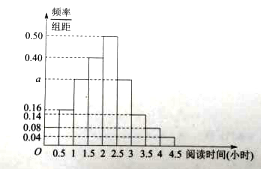
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)估计该校高一学生周末“阅读时间”的中位数;
(Ⅲ)用样本频率代替概率. 现从全校高一年级随机抽取![]() 名学生,其中有
名学生,其中有![]() 名学生“阅读时间”在
名学生“阅读时间”在![]() 小时内的概率为
小时内的概率为![]() ,其中
,其中![]() .当
.当![]() 取最大时,求
取最大时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com