Question

设函数f（x）=ax²+blnx，其中ab≠0．
证明：当ab＞0时，函数f（x）没有极值点；当ab＜0时，函数f（x）有且只有一个极值点，并求出极值．

Answer 1

分析：因为函数有没有极值点是由导函数等于0有没有根决定的，故转化为证ab＞0时导函数等于0没有根；ab＜0时，导函数有且只有一个根，且在根的两侧导函数不同号即可．

解答：证明：因为f（x）=ax²+blnx，ab≠0，所以f（x）的定义域为（0，+∞）．f'（x）=2ax+

b

x

=

2ax2+b

x

．
当ab＞0时，如果a＞0，b＞0，f'（x）＞0，f（x）在（0，+∞）上单调递增；
如果a＜0，b＜0，f'（x）＜0，f（x）在（0，+∞）上单调递减．
所以当ab＞0，函数f（x）没有极值点．
当ab＜0时，f′(x)=

2a(x+ - b 2a )(x- - b 2a )

x

令f'（x）=0，
得x1=-

- b 2a

∉(0，+∞)（舍去），x2=

- b 2a

∈(0，+∞)，
当a＞0，b＜0时，f'（x），f（x）随x的变化情况如下表：

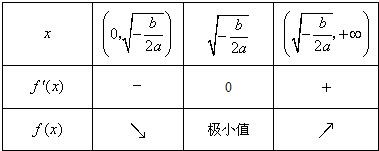
从上表可看出，
函数f（x）有且只有一个极小值点，极小值为f(

- b 2a

)=-

b

2

[1-ln(-

b

2a

)]．
当a＜0，b＞0时，f'（x），f（x）随x的变化情况如下表：

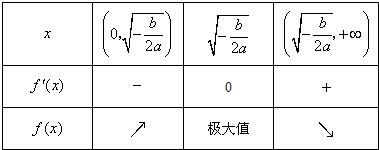
从上表可看出，
函数f（x）有且只有一个极大值点，极大值为f(

- b 2a

)=-

b

2

[1-ln(-

b

2a

)]．
综上所述，
当ab＞0时，函数f（x）没有极值点；
当ab＜0时，
若a＞0，b＜0时，函数f（x）有且只有一个极小值点，极小值为-

b

2

[1-ln(-

b

2a

)]．
若a＜0，b＞0时，函数f（x）有且只有一个极大值点，极大值为-

b

2

[1-ln(-

b

2a

)]．

点评：本题考查利用导函数来研究函数的极值以及对分类讨论思想的考查．分类讨论思想在数学中是非常重要的思想之一，所以希望能加强这方面的训练．