
【题目】在△ABC中,a![]() ,c
,c![]() ,________.(补充条件)
,________.(补充条件)
(1)求△ABC的面积;
(2)求sin(A+B).
从①b=4,②cosB![]() ,③sinA
,③sinA![]() 这三个条件中任选一个,补充在上面问题中并作答.
这三个条件中任选一个,补充在上面问题中并作答.
【答案】详见解析
【解析】
选择①(1)先由余弦定理求得cosC,进而求得sinC,由此求得面积;
(2)sin(A+B)=sinC,直接可以得出答案;
选择②(1)利用平方关系求得sinB,进而求得面积;
(2)先由余弦定理求得b,再由正弦定理求得sinC,进而得解;
选择③(1)先由平方关系求得cosA,再由余弦定理求得b,进而求得面积;
(2)由正弦定理可得![]() ,由此即可得解.
,由此即可得解.
选择①
(1)在△ABC中,因为![]() ,
,![]() ,b=4,
,b=4,
由余弦定理得![]() ,
,
因为C∈(0,π),所以![]() ,
,
所以![]() .
.
(2)在△ABC中,A+B=π﹣C.
所以![]() .
.
选择②
(1)因为![]() ,B∈(0,π),所以
,B∈(0,π),所以![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() .
.
(2)因为![]() ,
,![]() ,
,![]() ,
,
由b2=a2+c2﹣2accosB,得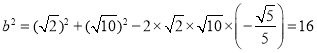 ,
,
解得b=4,
由![]() ,解得
,解得![]() ,
,
在△ABC中,A+B=π﹣C,![]() .
.
选择③
依题意,A为锐角,由![]() ,得
,得![]() ,
,
在△ABC中,因为![]() ,
,![]() ,
,![]() ,
,
由余弦定理a2=b2+c2﹣2bccosA,得![]() ,
,
解得b=2或b=4,
(1)当b=2时,![]() .
.
当b=4时,![]() .
.
(2)由![]() ,
,![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,
在△ABC中,A+B=π﹣C,![]() .
.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙、丁、戊5种在线教学软件,若某学校要从中随机选取3种作为教师“停课不停学”的教学工具,则其中甲、乙、丙至多有2种被选取的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为抛物线
为抛物线![]() 上不同的两点,且
上不同的两点,且![]() ,点
,点![]()
![]() 且
且![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
(2)过![]() 轴上一点
轴上一点 ![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 的准线上的射影分别为
的准线上的射影分别为![]() ,
,![]() 为
为![]() 的焦点,若
的焦点,若![]() ,求
,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an=![]() (n∈N*,n≥2),数列{bn}满足关系式bn=
(n∈N*,n≥2),数列{bn}满足关系式bn=![]() (n∈N*).
(n∈N*).
(1)求证:数列{bn}为等差数列;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系xOy中,椭圆![]() (a>b>0)的短轴长为
(a>b>0)的短轴长为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆的方程;
(2)斜率为1且经过椭圆的右焦点的直线交椭圆于P1、P2两点,P是椭圆上任意一点,若![]() (λ,μ∈R),证明:λ2+μ2为定值.
(λ,μ∈R),证明:λ2+μ2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为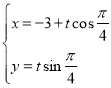 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 是曲线
是曲线![]() 上的任意一点,当点
上的任意一点,当点![]() 到直线
到直线![]() 的距离最大时,求经过点
的距离最大时,求经过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com