Question

【题目】底面为正方形的四棱锥S﹣ABCD，且SD⊥平面ABCD，SD= ，AB=1，线段SB上一M点满足 = ，N为线段CD的中点，P为四棱锥S﹣ABCD表面上一点，且DM⊥PN，则点P形成的轨迹的长度为（ ）
A.
B.
C.
D.2

Answer 1

【答案】B
【解析】解：以D为坐标原点，以DA，DC，DS为坐标轴建立空间直角坐标系，如图所示：

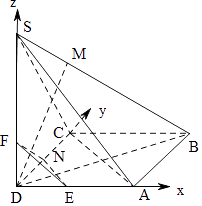
则B（1，1，0），S（0，0， ），N（0， ，0），D（0，0，0），M（ ， ， ），

取AD的中点E，则E（ ，0，0），∴ =（ ， ， ）， =（﹣ ， ，0），

∴ =0，即DM⊥EN，

在SD上取一点F，设F（0，0，a），则 =（﹣ ，0，a），

设DM⊥EF，则 ，即﹣ + =0，解得a= ，

∴DM⊥平面EFN，

∴P点轨迹为△EFN．

∵EF=FN= = ，EN= AC= ，

∴△EFN的周长为 = ．

故选：B．

【考点精析】掌握棱锥的结构特征是解答本题的根本，需要知道侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．