
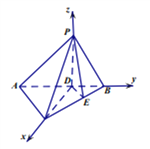
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.

【答案】(1)证明见解析;(2)30°.
【解析】试题分析:
(1)由条件可得![]() 为直角三角形,且
为直角三角形,且![]() .故由余弦定理可得
.故由余弦定理可得![]() ,所以
,所以![]() ,从而
,从而![]() ,又由条件可得
,又由条件可得![]() ,故
,故![]() 平面
平面![]() .(2)由
.(2)由![]() 两两互相垂直可建立空间直角坐标系,结合条件可求得平面
两两互相垂直可建立空间直角坐标系,结合条件可求得平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,根据两法向量夹角的余弦值可得锐二面角的大小.
的法向量,根据两法向量夹角的余弦值可得锐二面角的大小.
试题解析:
(1)证明:连![]() ,由题意知
,由题意知![]() .
.
![]()
![]()
∴![]()
在![]() 中,由余弦定理得
中,由余弦定理得
![]()
![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
又因为![]() ,
,
∴![]()
又![]()
,
![]()
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() 两两互相垂直,建立如图所示的空间直角坐标系
两两互相垂直,建立如图所示的空间直角坐标系![]() ,
,
由![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,知
,知![]() ,
,
则![]()
∴![]()
因为![]()
![]()
由(1)知![]()
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ∴
∴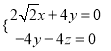 ,
,
令![]() ,则
,则![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
∴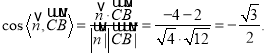
故平面![]() 与平面
与平面![]() 的锐二面角的余弦值为
的锐二面角的余弦值为![]() ,
,
所以平面![]() 与平面
与平面![]() 的锐二面角为
的锐二面角为![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣x,g(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数g(x)的单调性;
(2)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只袋中装有编号为1,2,3,…,n的n个小球,n≥4,这些小球除编号以外无任何区别,现从袋中不重复地随机取出4个小球,记取得的4个小球的最大编号与最小编号的差的绝对值为ξn , 如ξ4=3,ξ5=3或4,ξ6=3或4或5,记ξn的数学期望为f(n).
(1)求f(5),f(6);
(2)求f(n).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式﹣2<|x﹣1|﹣|x+2|<0的解集为M,a、b∈M,
(1)证明:| ![]() a+
a+ ![]() b|<
b|< ![]() ;
;
(2)比较|1﹣4ab|与2|a﹣b|的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() =1(a>b>0),作直线l交椭圆于P,Q两点,M为线段PQ的中点,O为坐标原点,设直线l的斜率为k1 , 直线OM的斜率为k2 , k1k2=﹣
=1(a>b>0),作直线l交椭圆于P,Q两点,M为线段PQ的中点,O为坐标原点,设直线l的斜率为k1 , 直线OM的斜率为k2 , k1k2=﹣ ![]() .
.
(1)求椭圆C的离心率;
(2)设直线l与x轴交于点D(﹣ ![]() ,0),且满足
,0),且满足 ![]() =2
=2 ![]() ,当△OPQ的面积最大时,求椭圆C的方程.
,当△OPQ的面积最大时,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等比数列{an}满足a1 , 2a2 , a3+6成等差数列,且a42=9a1a5 ,
(1)求数列{an}的通项公式;
(2)设bn=( ![]() an+1)an , 求数列{bn}的前n项和Tn .
an+1)an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高中毕业班有男生900人,女生600人,学校为了对高三学生数学学习情况进行分析,从高三年级按照性别进行分层抽样,抽取200名学生成绩,统计数据如表所示:
分数段(分) | [50,70) | [70,90) | [90,110) | [110,130) | [130,150) | 总计 |
频数 | 20 | 40 | 70 | 50 | 20 | 200 |
(1)若成绩90分以上(含90分),则成绩为及格,请估计该校毕业班平均成绩及格学生人数;
(2)如果样本数据中,有60名女生数学成绩合格,请完成如下数学成绩与性别的列联表,并判断是否有90%的把握认为“该校学生的数学成绩与性别有关”.
女生 | 男生 | 总计 | |
及格人数 | 60 | ||
不及格人数 | |||
总计 |
参考公式:K2= ![]() .
.
P(K2≥k0) | 0.10 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com