
【题目】已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在y=x2的函数图象上.
(1)求数列{an}的通项公式;
(2)若bn=(-1)n+1anan+1,求数列{bn}的前100项和T100.
【答案】(1)an=2n-1(2)-20200
【解析】
(1)点(n,Sn)(n∈N*)在y=x2的函数图象上.Sn=n2,可得:n≥2时,an=Sn-Sn-1.n=1时,a1=1.即可得出..
(2)bn=(-1)n+1anan+1,可得b2n-1+b2n=a2n-1a2n-a2na2n+1=-4(4n-1).利用等差数列的求和公式即可得出.
(1)点(n,Sn)(n∈N*)在y=x2的函数图象上.
∴Sn=n2,
可得:n≥2时,an=Sn﹣Sn﹣1=n2﹣(n﹣1)2=2n﹣1.
n=1时,a1=1.
可得:an=2n﹣1.
(2)bn=(﹣1)n+1anan+1,
∴b2n﹣1+b2n=a2n﹣1a2n﹣a2na2n+1=(4n﹣1)(4n﹣3﹣4n﹣1)=﹣4(4n﹣1).
∴数列{bn}的前100项和T100=﹣4![]() 20200.
20200.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“荆、荆、襄、宜七校联考”正在如期开展,组委会为了解各所学校学生的学情,欲从四地选取200人作样本开展调研.若来自荆州地区的考生有1000人,荆门地区的考生有2000人,襄阳地区的考生有3000人,宜昌地区的考生有2000人.为保证调研结果相对准确,下列判断正确的有( )
①用分层抽样的方法分别抽取荆州地区学生25人、荆门地区学生50人、襄阳地区学生75人、宜昌地区学生50人;
②可采用简单随机抽样的方法从所有考生中选出200人开展调研;
③宜昌地区学生小刘被选中的概率为![]() ;
;
④襄阳地区学生小张被选中的概率为![]() .
.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在道路边安装路灯,路面![]() 宽
宽![]() ,灯柱
,灯柱![]() 高14
高14![]() ,灯杆
,灯杆![]() 与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线
与地面所成角为30°.路灯采用锥形灯罩,灯罩轴线![]() 与灯杆
与灯杆![]() 垂直,轴线
垂直,轴线![]() ,灯杆
,灯杆![]() 都在灯柱
都在灯柱![]() 和路面宽线
和路面宽线![]() 确定的平面内.
确定的平面内.

(1)当灯杆![]() 长度为多少时,灯罩轴线
长度为多少时,灯罩轴线![]() 正好通过路面
正好通过路面![]() 的中线?
的中线?
(2)如果灯罩轴线AC正好通过路面![]() 的中线,此时有一高2.5
的中线,此时有一高2.5 ![]() 的警示牌直立在
的警示牌直立在![]() 处,求警示牌在该路灯灯光下的影子长度.
处,求警示牌在该路灯灯光下的影子长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,离心率
,离心率![]() .
.
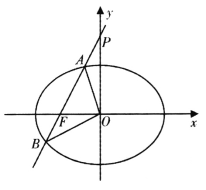
(I)求椭圆C的标准方程;
(II)已知直线![]() 交椭圆C于A,B两点.
交椭圆C于A,B两点.
①若直线![]() 经过椭圆C的左焦点F,交y轴于点P,且满足
经过椭圆C的左焦点F,交y轴于点P,且满足![]() .求证:
.求证:![]() 为定值;
为定值;
②若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,03,![]() ,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
,49,50的50个个体组成,利用随机数表(以下选取了随机数表中的第1行和第2行)选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取,则选出来的第4个个体的编号为( )
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且过点
的焦点重合,且过点![]() .过点
.过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 为椭圆的左顶点.
为椭圆的左顶点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com