练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若 是函数 图象的一条对称轴，当ω取最小正数时（ ）
    A.f（x）在 单调递减
    B.f（x）在 单调递增
    C.f（x）在 单调递减
    D.f（x）在 单调递增

    【答案】D
    【解析】解： =2sin（ωx+ ）

    ∴函数f（x）图象的对称轴方程：ωx+ = +2kπ（k∈Z）

    ∵ 是f（x）图象的一条对称轴，

    ∴ω + = +2kπ，得ω=2+6kπ，（k∈Z）

    当k=0时，ω取最小正数2，此时f（x）=（2x+ ）

    ∴f（x）的单调增区间为（﹣ +kπ， +kπ），单调减区间为（ +kπ， +kπ）

    对照ABCD各选项，可知只有D符合题意

    故选：D

    【考点精析】认真审题，首先需要了解两角和与差的正弦公式(两角和与差的正弦公式：)，还要掌握正弦函数的单调性(正弦函数的单调性：在上是增函数；在上是减函数)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）在R上存在导数f′（x），x∈R，有f（﹣x）+f（x）=x2 ， 在（0，+∞）上f′（x）＜x，若f（4﹣m）﹣f（m）≥8﹣4m．则实数m的取值范围为（ ）
    A.[﹣2，2]
    B.[2，+∞）
    C.[0，+∞）
    D.（﹣∞，﹣2]∪[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆 （a＞b＞0）的左右顶点分别是A（﹣ ，0），B（ ，0），离心率为 ．设点P（a，t）（t≠0），连接PA交椭圆于点C，坐标原点是O．
    （Ⅰ）证明：OP⊥BC；
    （Ⅱ）若三角形ABC的面积不大于四边形OBPC的面积，求|t|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图直三棱柱ABC﹣A1B1C1 中AC=2AA1 ， AC⊥BC，D、E 分别为A1C1、AB 的中点．求证：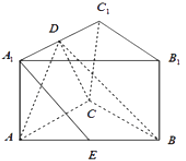

    （1）AD⊥平面BCD
    （2）A1E∥平面BCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b，c均为正数，且a+2b+3c=9．求证： + + ≥ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在边长为2的正三角形△ABC中，D为BC的中点，E，F分别在边CA，AB上．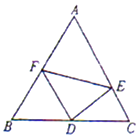
    （1）若 ，求CE的长；
    （2）若∠EDF=60°，问：当∠CDE取何值时，△DEF的面积最小？并求出面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国南宋时期的数学家秦九韶是普州（现四川省安岳县）人，秦九韶在其所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一例，则输出的S的值为（ ）
    A.4
    B.﹣5
    C.14
    D.﹣23

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，sin = ，AB=2，点D在线段AC上，且AD=2DC，BD= ，则cosC= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ﹣ ，若对任意的x1 ， x2∈[1，2]，且x1≠x2时，[|f（x1）|﹣|f（x2）|]（x1﹣x2）＞0，则实数a的取值范围为（ ）
    A.[﹣ ， ]
    B.[﹣ ， ]
    C.[﹣ ， ]
    D.[﹣e2 ， e2]

    查看答案和解析>>

    同步练习册答案