
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求
,求![]() 与平面所成角的正弦值.
与平面所成角的正弦值.
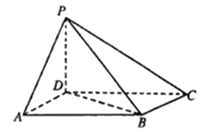
【答案】(1) 见解析(2) ![]()
【解析】试题分析:(1)推导出BC⊥BD,PD⊥BC,从而BC⊥平面PBD,由此能证明平面PBC⊥平面PBD.
(2)由BC⊥平面PBD,得∠PBD即为二面角P﹣BC﹣D的平面角,即![]() ,从而BD=
,从而BD=![]() ,PD=
,PD=![]() ,分别以DA、DB、DP为x轴、y轴、z轴建立空间直角坐标系,利用向量法能求出AP与平面PBC所成角的正弦值.
,分别以DA、DB、DP为x轴、y轴、z轴建立空间直角坐标系,利用向量法能求出AP与平面PBC所成角的正弦值.
试题解析:
(1)∵![]() ,∴
,∴![]()
又∵![]() 底面
底面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]()
而![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)由(1)所证, ![]() 平面
平面![]()
所以![]() 即为二面角
即为二面角![]() 的平面角,即
的平面角,即![]() .
.
而![]() ,所以
,所以![]()
因为底面![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
分别以![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
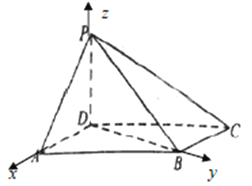
则![]() ,
,
所以![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() 即
即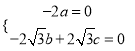
令![]() ,则
,则![]() ,
,
所以![]()
∴![]() 与平面所成角的正弦值
与平面所成角的正弦值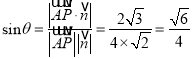 .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】如图C,D是以AB为直径的圆上的两点,![]() ,F是AB上的一点,且
,F是AB上的一点,且![]() ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知![]()

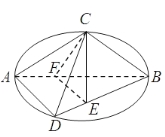
(1)求证:AD![]() 平面BCE
平面BCE
(2)求证:AD//平面CEF;
(3)求三棱锥A-CFD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于圆锥曲线的命题中
①设![]() 是两个定点,
是两个定点, ![]() 为非零常数,若
为非零常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线的一支;②过定圆
的轨迹为双曲线的一支;②过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
, ![]() 为坐标原点,若
为坐标原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;③方程
的轨迹为椭圆;③方程![]() 的两根可分别作为椭圆和双曲线的离心率;④双曲线
的两根可分别作为椭圆和双曲线的离心率;④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中, ![]() 是椭圆
是椭圆![]()
![]() 的右顶点,
的右顶点, ![]() 是上顶点,
是上顶点, ![]() 是椭圆位于第三象限上的任一点,连接
是椭圆位于第三象限上的任一点,连接![]() ,
, ![]() 分别交坐标轴于
分别交坐标轴于![]() ,
, ![]() 两点.
两点.
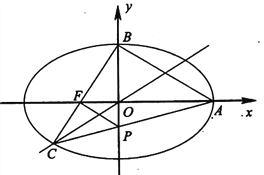
(1)若点![]() 为左焦点且直线
为左焦点且直线![]() 平分线段
平分线段![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)求证:四边形![]() 的面积是定值.
的面积是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30人,则每人收取培训费1000元;若参加培训的员工人数超过30人,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算:公司此次培训的总费用最多需要多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com