
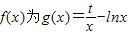 (t为实数)的一个“上界函数”,求t的取值范围;
(t为实数)的一个“上界函数”,求t的取值范围;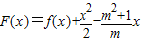 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.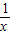 等于一个关系式,设y=x+
等于一个关系式,设y=x+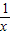 ,且x大于0小于2,画出该函数的图象,如图所示,然后分m=1,m大于
,且x大于0小于2,画出该函数的图象,如图所示,然后分m=1,m大于 小于2,m大于0小于等于
小于2,m大于0小于等于 和m大于等于2,四种情况,根据函数的图象,即可得到相应区间上极值点的个数.
和m大于等于2,四种情况,根据函数的图象,即可得到相应区间上极值点的个数.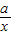 ,由切线方程知f′(1)=1,所以a=1,
,由切线方程知f′(1)=1,所以a=1,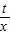 -lnx≤lnx恒成立,
-lnx≤lnx恒成立,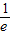 )时,h′(x)<0,所以h(x)在(0,
)时,h′(x)<0,所以h(x)在(0,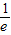 )上是减函数,
)上是减函数,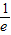 ,+∞)时,h′(x)>0,所以h(x)在(
,+∞)时,h′(x)>0,所以h(x)在(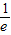 ,+∞)上是增函数,
,+∞)上是增函数,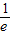 )=-
)=-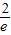 ,所以t≤-
,所以t≤-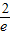 ;
;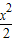 -
-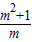 x,所以F′(x)=
x,所以F′(x)=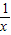 +x-
+x-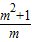 ,
,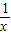 +x=
+x=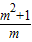 ,令y=x+
,令y=x+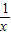 ,x∈(0,2),
,x∈(0,2),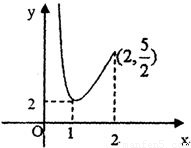
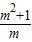 =2,即m=1时,F′(x)=0在区间(0,2)上只有一个根1,且在1的两侧,
=2,即m=1时,F′(x)=0在区间(0,2)上只有一个根1,且在1的两侧,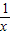 >2,即在1的两侧F′(x)同正,此时F(x)在(0,2)上无极值点;
>2,即在1的两侧F′(x)同正,此时F(x)在(0,2)上无极值点;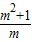 <
< ,即
,即 <m<2,且m≠1时,F′(x)=0在区间(0,2)上有两个不等根,
<m<2,且m≠1时,F′(x)=0在区间(0,2)上有两个不等根,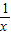 -
-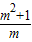 都是异号的,
都是异号的,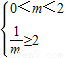 ,即0<m≤
,即0<m≤ 时,方程在区间(0,2)上只有一个根m,
时,方程在区间(0,2)上只有一个根m,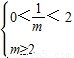 ,即m≥2时,方程在区间(0,2)上只有一个根
,即m≥2时,方程在区间(0,2)上只有一个根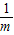 ,
,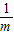 两侧的符号不同,
两侧的符号不同, )∪[2,+∞)时,函数F(x)在区间(0,2)上有一个极值点;
)∪[2,+∞)时,函数F(x)在区间(0,2)上有一个极值点; ,1)∪(1,2)时,函数F(x)在区间(0,2)上有两个极值点.
,1)∪(1,2)时,函数F(x)在区间(0,2)上有两个极值点.

科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com