
【题目】已知函数![]() ,
,![]() .
.
![]() 当
当![]() 时,
时,![]() ,求实数a的取值范围;
,求实数a的取值范围;
![]() 当
当![]() 时,曲线
时,曲线![]() 和曲线
和曲线![]() 是否存在公共切线?并说明理由.
是否存在公共切线?并说明理由.
【答案】(1)![]() ;(2)存在公共切线,理由详见解析.
;(2)存在公共切线,理由详见解析.
【解析】
(1)构造函数![]() ,求出其最大值,解不等式即可得到实数
,求出其最大值,解不等式即可得到实数![]() 的取值范围;
的取值范围;
(2)假设存在这样的直线![]() 且直线
且直线![]() 与曲线和曲线
与曲线和曲线![]() 分别相切与点
分别相切与点![]() .分别求出两条切线方程,根据斜率与纵截距建立方程组,减元后得到
.分别求出两条切线方程,根据斜率与纵截距建立方程组,减元后得到![]() ,构造新函数研究单调性与极值即可.
,构造新函数研究单调性与极值即可.
解:![]() 令
令![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ,若
,若![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
所以![]() 是
是![]() 的极大值点,也是
的极大值点,也是![]() 的最大值点,即
的最大值点,即![]() .
.
若![]() 恒成立,则只需
恒成立,则只需![]() ,解得
,解得![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.
![]() 假设存在这样的直线
假设存在这样的直线![]() 且与曲线
且与曲线![]() 和曲线
和曲线![]() 分别相切与点
分别相切与点![]() .
.
由![]() ,得
,得![]() .
.
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
同理可得,
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
所以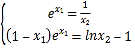 则
则![]() ,即
,即![]()
构造函数![]()
![]()
存在直线![]() 与曲线
与曲线![]() 和曲线
和曲线![]() 相切,
相切,
等价于函数![]() 在
在![]() 上有零点
上有零点
对于![]() .
.
当![]() 时,
时,![]() ,
,![]() 在上单调递增.
在上单调递增.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() 在
在![]() 上是减函数.
上是减函数.
又![]() ,,所以存在
,,所以存在![]() ,使得
,使得![]() ,即
,即![]() .
.
且当![]() ,
,![]() 时,当
时,当![]() 时,
时,![]() .
.
综上,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
所以![]() 是
是![]() 的极大值,也是最大值,且
的极大值,也是最大值,且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 在
在![]() 内和
内和![]() 内各有一个零点.
内各有一个零点.
故假设成立,即曲线![]() 和曲线
和曲线![]() 存在公共切线.
存在公共切线.


科目:高中数学 来源: 题型:
【题目】某机构组织语文、数学学科能力竞赛,按照一定比例淘汰后,颁发一二三等奖.现有某考场的两科考试成绩数据统计如下图所示,其中数学科目成绩为二等奖的考生有![]() 人.
人.
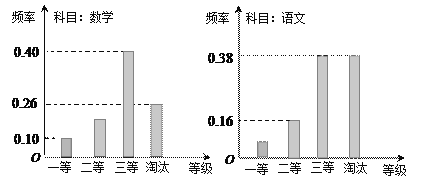

(Ⅰ)求该考场考生中语文成绩为一等奖的人数;
(Ⅱ)用随机抽样的方法从获得数学和语文二等奖的学生中各抽取![]() 人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
人,进行综合素质测试,将他们的综合得分绘成茎叶图,求样本的平均数及方差并进行比较分析;
(Ⅲ)已知本考场的所有考生中,恰有![]() 人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取
人两科成绩均为一等奖,在至少一科成绩为一等奖的考生中,随机抽取![]() 人进行访谈,求两人两科成绩均为一等奖的概率.
人进行访谈,求两人两科成绩均为一等奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法错误的是( )
A.复数![]() 满足
满足![]() ,则复数
,则复数![]() 在复平面上对应的点的轨迹为直线.
在复平面上对应的点的轨迹为直线.
B.![]() 为
为![]() 上连续可导的函数,若
上连续可导的函数,若![]() ,则
,则![]() 为极值点.
为极值点.
C.若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.![]() 为抛物线
为抛物线![]() 的两点,
的两点,![]() 为坐标原点,若
为坐标原点,若![]() ,则直线
,则直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为![]() 的样本,测量树苗高度(单位:
的样本,测量树苗高度(单位:![]() ),经统计,其高度均在区间
),经统计,其高度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成
分成![]() 组,制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.
组,制成如图所示的频率分布直方图.其中高度为27cm及以上的树苗为优质树苗.
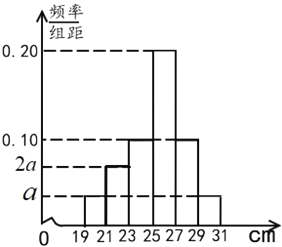
(1)求图中![]() 的值;
的值;
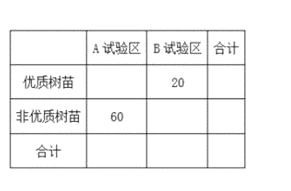
(2)已知所抽取这![]() 棵树苗来自于
棵树苗来自于![]() 两个试验区,部分数据如下列联表:将列联表补充完整,并判断是否有
两个试验区,部分数据如下列联表:将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() 两个试验区有关系,并说明理由;
两个试验区有关系,并说明理由;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: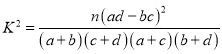 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间x与乘客等候人数y之间的关系,经过调查得到如下数据:
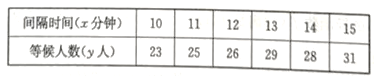
调查小组先从这6组数据中选取4组数据求线性回归方程,再用剩下的2组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数y的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
与实际等候人数y的差,若差值的绝对值不超过1,则称所求方程是“恰当回归方程”.
(1)若选取的是后面4组数据,求y关于x的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(2)为了使等候的乘客不超过35人,试用(1)中方程估计间隔时间最多可以设置为多少(精确到整数)分钟?
附:对于一组数据(x1,y1),(x2,y2),……,(xn,yn),其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
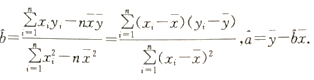
查看答案和解析>>
科目:高中数学 来源: 题型:
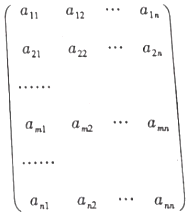
【题目】在如图所示的数阵中每一行从左到右均是首项为1,项数为n的等差数列,设第![]() 行的等差数列中的第k项为
行的等差数列中的第k项为![]() 2,3,
2,3,![]() ,
,![]() ,公差为
,公差为![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 也成等差数列.
也成等差数列.
![]() Ⅰ
Ⅰ![]() 求
求![]() ;
;
![]() Ⅱ
Ⅱ![]() 求
求![]() 关于m的表达式;
关于m的表达式;
![]() Ⅲ
Ⅲ![]() 若数阵中第i行所有数之和
若数阵中第i行所有数之和![]() ,第j列所有数之和为
,第j列所有数之和为![]() ,是否存在i,j满足
,是否存在i,j满足![]() ,使得
,使得![]() 成立?若存在,请求出i,j的一组值;若不存在,请说明理由.
成立?若存在,请求出i,j的一组值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2014·长春模拟)对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表:
甲 | 27 | 38 | 30 | 37 | 35 | 31 |
乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(1)画出茎叶图.
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com