【题目】在△ABC中，a，b，c分别是角A，B，C的对边，且8sin2 
．
（1）求角A的大小；
（2）若a= 
，b+c=3，求b和c的值．
科目：高中数学 来源： 题型：
【题目】设 
，曲线y=f（x）在点（1，f（1））处的切线与直线x+y+1=0垂直．
（1）求a的值；
（2）若对于任意的x∈[1，+∞），f（x）≤m（x﹣1）恒成立，求m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在某单位的职工食堂中，食堂每天以3元/个的价格从面包店购进面包，然后以5元/个的价格出售．如果当天卖不完，剩下的面包以1元/个的价格卖给饲料加工厂．根据以往统计资料，得到食堂每天面包需求量的频率分布直方图如下图所示．食堂某天购进了90个面包，以x（单位：个，60≤x≤110）表示面包的需求量，T（单位：元）表示利润．
（Ⅰ）求T关于x的函数解析式；
（Ⅱ）根据直方图估计利润T不少于100元的概率；
（Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中间值的概率（例如：若需求量x∈[60，70），则取x=65，且x=65的概率等于需求量落入[60，70）的频率），求T的分布列和数学期望．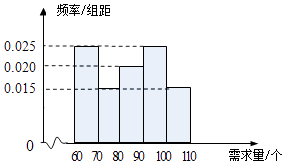
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果对一切实数x、y，不等式 
﹣cos2x≥asinx﹣ 
恒成立，则实数a的取值范围是（ ）
A.（﹣∞， 
]
B.[3，+∞）
C.[﹣2 
，2 ]
D.[﹣3，3]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地要建造一个边长为2（单位：km）的正方形市民休闲公园OABC，将其中的区域ODC开挖成一个池塘，如图建立平面直角坐标系后，点D的坐标为（1，2），曲线OD是函数y=ax2图象的一部分，对边OA上一点M在区域OABD内作一次函数y=kx+b（k＞0）的图象，与线段DB交于点N（点N不与点D重合），且线段MN与曲线OD有且只有一个公共点P，四边形MABN为绿化风景区：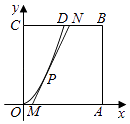 
（1）求证：b=﹣ 
；
（2）设点P的横坐标为t，①用t表示M、N两点坐标；②将四边形MABN的面积S表示成关于t的函数S=S（t），并求S的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将函数f（x）=cos（ωx+φ）（ω＞0，﹣ 
＜φ＜ ）图象上每一点的横坐标伸长为原来的2倍（纵坐标不变），再向右平移 
个单位长度得到y=cosx的图象，则函数f（x）的单调递增区间为（ ）
A.[kπ﹣ 
，kπ+ 
]（k∈Z）
B.[kπ﹣ 
，kπ﹣ 
]（k∈Z）
C.[4kπ﹣ 
，kπ﹣ ]（k∈Z）
D.[4kπ﹣ ，kπ+ 
]（k∈Z）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C1的参数方程为 
（t为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2cosθ．
（Ⅰ）把C1的参数方程化为极坐标方程；
（Ⅱ）求C1与C2交点的极坐标（ρ≥0，0≤θ＜2π）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在R上的奇函数f（x）和偶函数g（x）满足f（x）=2g（x）+ 
，若f（ 
）+f（cos2θ）＜f（π）﹣f（ 
），则θ的取值范围是（ ）
A.（2kπ+ 
，2kπ+ 
），k∈Z
B.（2kπ﹣ ，2kπ）∪（2kπ，2kπ+π）∪（2kπ+π，2kπ+ 
π），k∈Z
C.（2kπ﹣ ，2kπ﹣ ），k∈Z
D.（2kπ﹣ 
，2kπ﹣π）∪（2kπ﹣π，2kπ）∪（2kπ，2kπ+ ），k∈Z
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）的导函数f′（x），满足（x﹣2）[f′（x）﹣f（x）]＞0，且f（4﹣x）=e4﹣2xf（x），则下列关于 f（x）的命题正确的是（ ）
A.f（3）＞e2f（1）
B.f（3）＜ef（2）
C.f（4）＜e4f（0）
D.f（4）＜e5f（﹣1）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
